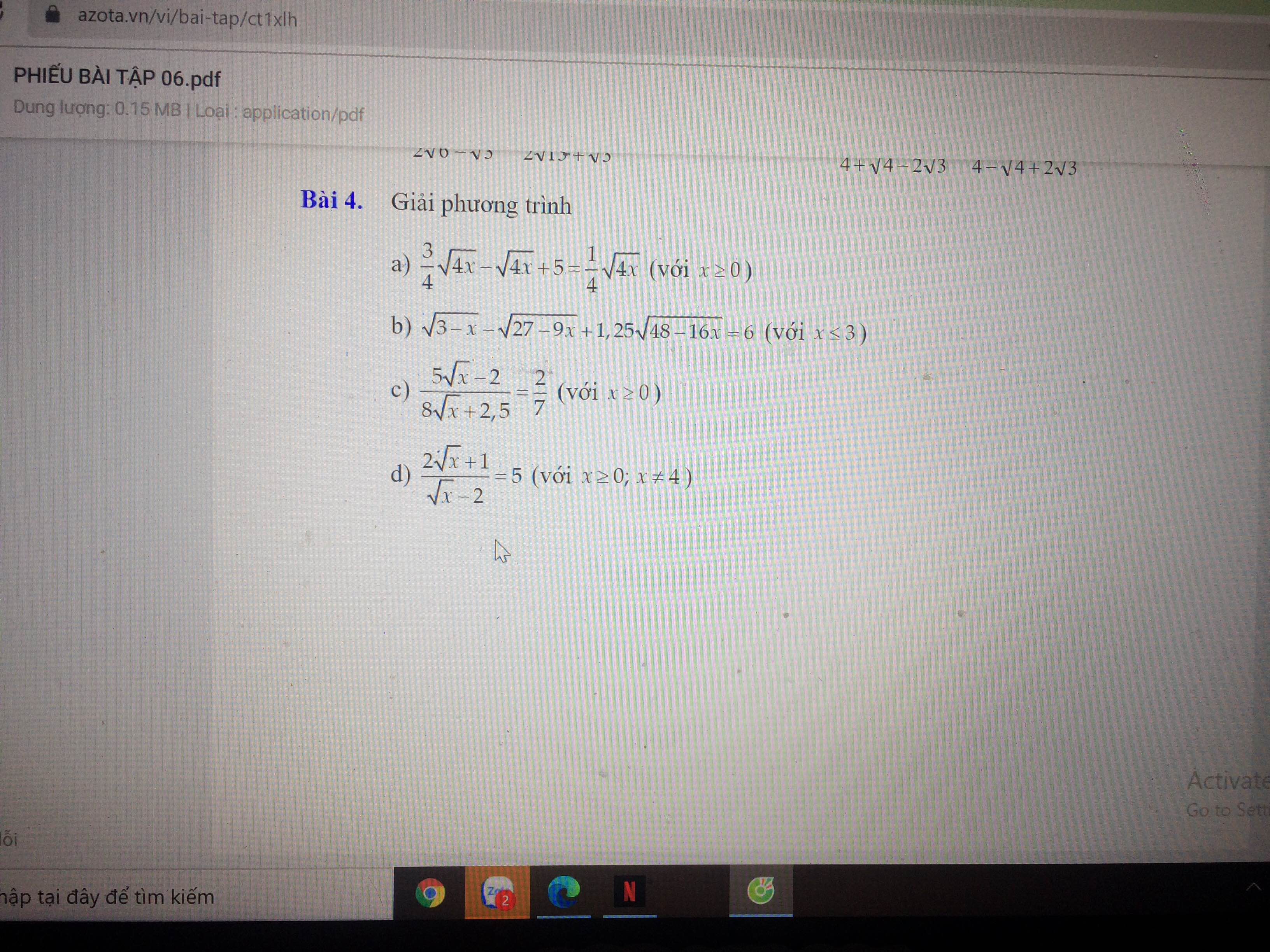
Giúp e giải bài 4 được kg ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
a: \(\dfrac{2-\sqrt{3}}{3\sqrt{6}}=\dfrac{2\sqrt{6}-3\sqrt{2}}{18}\)
b: \(\dfrac{1}{\sqrt{3}+\sqrt{2}}=\sqrt{3}-\sqrt{2}\)

Bài 3:
\(a,=\dfrac{53\left(9+2\sqrt{7}\right)}{53}+2\sqrt{7}-5=9+2\sqrt{7}+2\sqrt{7}-5=4+4\sqrt{7}\)
a: Sửa đề: \(\dfrac{53}{9-2\sqrt{7}}+2\sqrt{7}-5\)
\(=9+2\sqrt{7}+2\sqrt{7}-5\)
\(=4\sqrt{7}+4\)

Bài 1:
a: \(-xy\sqrt{\dfrac{y}{x}}=-xy\cdot\dfrac{\sqrt{xy}}{x}=-y\sqrt{xy}\)
b: \(\sqrt{\dfrac{-3x^2}{35}}=\dfrac{\sqrt{105}x}{35}\)

bài 3:
b: \(\dfrac{2}{\sqrt{3}+1}+\dfrac{1}{2-\sqrt{3}}+\dfrac{6}{3+\sqrt{3}}\)
\(=\sqrt{3}-1+2+\sqrt{3}+\sqrt{3}-1\)
\(=3\sqrt{3}\)


a, xét tg HBA và tg ABC có:
góc BHA=goc BAC=90 độ
góc ABC_ chung
\(\Rightarrow\)tg HBA\(\sim\)tg ABC(g.g)
b, từ tg HBA\(\sim\)tg ABC(cmt) => BH/AB=AB/BC\(\Rightarrow\) AB2=BH.BC
mà AB=BE(gt) \(\Rightarrow\)BE2=BH.BC
c, áp dụng định lý pytago vào tam giác ABC vuông tại A =>BC=5cm
từ tg HBA\(\sim\)tg ABC(cmt)=> AH/AC=AB/BC
=> AH/4=3/5 => ah=2,4cm
d, tg ABC có BD là tia p/g =>AD/DC=AB/BC( tính chất đường phân giác trong tam giác)
=>AD/DC=3/5 => AD/3=DC/5
áp dụng tính chất dãy tỉ sô bằng nhau ta có:
=> AD/3=DC/5= AD+DC/3+5=AC/8=4/8=1/2
từ DC/5=1/2 \(\Rightarrow\)DC=2,5cm
xét tg EDB và tg ADB có:
BD_ cạnh chung
góc ABD=gocEBD
BE=AB(gt)
\(\Rightarrow\) tg EDB = tg ADB (c.g.c)
\(\Rightarrow\)góc ABD=goc BED=90 độ
xét tg CED và tg CABcó:
góc CED=gocBAC=90 độ
góc C_ góc chung
\(\Rightarrow\) tgCED \(\sim\) tg CAB (g.g)
tỉ số đồng dạng là DC/BC=2,5/5=1/2
\(\Rightarrow\)SCED/SABC =(1/2)2 =1/4

Bài 4 :
a) Xét \(\Delta\) ABD và \(\Delta\) ACE, ta có :
\(\widehat{BAD}\) = \(\widehat{CAE}\) (AD là đường phân giác)
\(\widehat{ABD}\) = \(\widehat{ACE}\) (gt)
\(\Rightarrow\) \(\Delta\) ABD \(\sim\) \(\Delta\) ACE (g.g)
b) \(\Delta\) ABD \(\sim\) \(\Delta\) ACE (câu a) \(\Rightarrow\) \(\widehat{ADB}\) = \(\widehat{AEC}\)
Mà \(\widehat{CED}\) = 180o - \(\widehat{CEA}\) ; \(\widehat{CDE}\) = 180o - \(\widehat{ADB}\) \(\Rightarrow\) \(\widehat{CED}\) = \(\widehat{CDE}\)
\(\Rightarrow\) \(\Delta\) CDE cân tại C










