Cho hàm số bậc nhất \(y=\left(2-a\right)x+a\). Biết đồ thị hàm số đi qua điểm M(3;1);, hàm số đồng biến hay nghịch biến trên R? Vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 9 2023
a) Vì đồ thị hàm số đi qua điểm \(M\left( {1; - 2} \right)\)nên ta có:
\( - 2 = a.1 - 4 \Leftrightarrow a = - 2 + 4 = 2\)
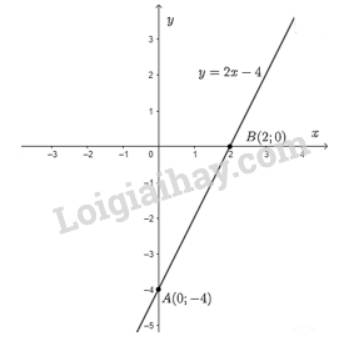
Hàm số cần tìm là \(y = 2x - 4\) có hệ số góc \(a = 2\).
b) Cho \(x = 0 \Rightarrow y = - 4\) ta được điểm \(A\left( {0; - 4} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{4}{2} = 2\) ta được điểm \(B\left( {2;0} \right)\) trên \(Ox\).
Đồ thị hàm số là đường thẳng đi qua hai điểm \(A\) và \(B\).
30 tháng 8 2023
Thay A(0,1) vào hàm số y ta có:
\(\left(m-3\right).4+3m-1=1\Leftrightarrow4m-12+3m-1=0\)
\(\Leftrightarrow7m-13=0\Leftrightarrow7m=13\Leftrightarrow m=\dfrac{13}{7}\)
23 tháng 12 2021
a: Để hàm số là hàm số bậc nhất thì 2m-3<>0
hay m<>3/2
b: Để hàm số đồng biến thì 2m-3>0
hay m>3/2
Để hàm số nghịch biến thì 2m-3<0
hay m<3/2
CM
23 tháng 6 2017
Hàm số y = ax + 3 là hàm số bậc nhất nên a ≠ 0
a) Đồ thị của hàm số đi qua điểm A(2; 6) nên:
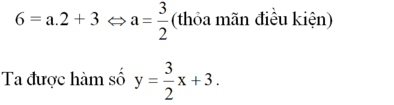
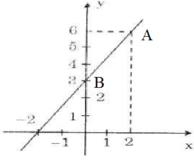
b) Vẽ đồ thị:
- Cho x = 0 thì y = 3 ta được B(0; 3).
Nối A, B ta được đồ thị hàm số
17 tháng 12 2021
1: Để hai đường thẳng song song thì 2m-1=-5
hay m=-2
ĐTHS đi qua \(M\left(3;1\right)\Rightarrow Thay\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\Rightarrow1=\left(2-a\right)3+a\Leftrightarrow a=\frac{5}{2}\)
Ta có: \(a=\frac{5}{2}>0\rightarrow HS\) đồng biến trên R