Giải giúp mình phần b. Xin cảm ơn!
Cho đường tròn tâm O bán kính R. Từ điểm C nằm ngoài đường tròn kẻ hai tiếp tuyến CA, CB và cát tuyến CMN với đường tròn (O) (A, B là hai tiếp điểm, M là điểm nằm giữa C và N). Gọi H là giao điểm của CO và AB
a) Chứng minh tứ giác AOBC nội tiếp
b) Tiếp tuyến tại M của đường tròn (O) cắt CA, CB theo thứ tự E, F. Đường thẳng vuông góc với CO tại O cắt CA, CB theo thứ tự tại P và Q. Chứng minh PE. QF có giá trị không đổi khi M thay đổi trên cung nhỏ AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
b: Xét ΔMAC và ΔMDA có
góc MAC=góc MDA
góc AMC chung
=>ΔMAC đồng dạng với ΔMDA
=>MA/MD=MC/MA
=>MA^2=MD*MC

c) ký hiệu các góc QOB, BOF, FOM, MOC, COE, EOA, AOP lần lượt là O1, O2, O3, O4, O5, O6, O7
Dễ thấy O5+O6+O7=90 mà O6=O4+O5 nên suy ra 2O5+O4+O7=90 (1)
tương tự 2O2+O1+O4=90 (vì O2=O3) (2).
mặt khác O7=O1 vì cùng phụ với 2 góc P và Q là 2 góc bằng nhau
Từ đó ta có O2=O5
lại có O2+OFQ =90
O5+POE=90 suy ra OFQ =POE (dpcm)
d) tam giác PEO đồng dạng với tam giác QOF nên suy ra PE.QF=OP.OQ=OP^2
Áp dụng bđt Cosi ta có PE+QF>= 2 căn PE.QF=2.căn OP^2=2OP=PQ (dpcm)

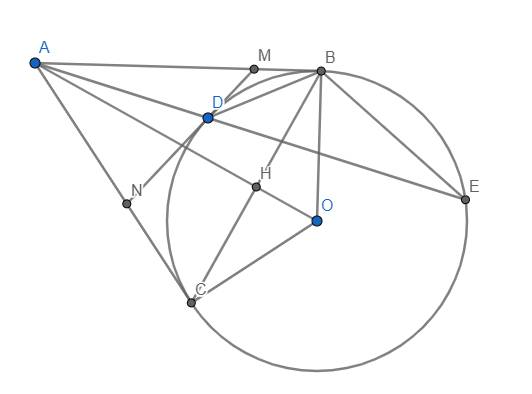
a) Do AB là tiếp tuyến của (O) tại B nên \(\widehat{ABO}=90^o\). CMTT, ta có \(\widehat{ACO}=90^o\) \(\Rightarrow\widehat{ABO}+\widehat{ACO}=180^o\) \(\Rightarrow\) Tứ giác ABOC nội tiếp (đpcm).
b) Theo tính chất 2 tiếp tuyến cắt nhau, ta có \(AO\perp BC\). Tam giác ABO vuông tại B, có đường cao BH nên \(AB^2=AH.AO\)
Mặt khác, lại có \(\widehat{ABD}=\widehat{ACB}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung đó) nên \(\Delta ABD~\Delta AEB\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AE}=\dfrac{AD}{AB}\) \(\Rightarrow AB^2=AD.AE\)
Từ đó dễ dàng suy ra \(AD.AE=AH.AO\)
c) Do tính chất của 2 tiếp tuyến cắt nhau nên \(\left\{{}\begin{matrix}MD=MB\\ND=NC\end{matrix}\right.\)
Do đó \(C_{AMN}=AM+AN+MN\)
\(=AM+AN+\left(MD+ND\right)\)
\(=\left(AM+MD\right)+\left(AN+ND\right)\)
\(=\left(AM+MB\right)+\left(AN+NC\right)\)
\(=AB+AC\)
\(=2AB\)
Lại có \(AB=\sqrt{AO^2-R^2}=\sqrt{6^2-3,6^2}=4,8cm\)
\(\Rightarrow C_{AMN}=2AB=2.4,8=9,6cm\)
