câu1:cho phương trình bậc hai:X2+4X-m+3=0(1). Tìm m để
1)Pt(1) có hai nghiệm trái dấu
2) Pt (1) có hai nghiệm x1,x2, thoả mãn X21+X22=16
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c) Để phương trình (1) có hai nghiệm x1 và x2 ⇔ Δ' ≥ 0 ⇔ 4 - m ≥ 0 ⇔ m ≤ 4
Theo Vi-et ta có: 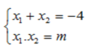
Ta có: x 1 2 + x 2 2 = 10 ⇔ x 1 + x 2 2 - 2x1x2 = 10
⇔ - 4 2 - 2m = 10 ⇔ 16 - 2m = 10 ⇔ m = 3 (TM)
Vậy với m = 3 thì phương trình (1) có hai nghiệm thõa mãn: x 1 2 + x 2 2 = 10

\(\Delta=9-4\left(k-1\right)=13-4k\ge0\Rightarrow k\le\dfrac{13}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=k-1\end{matrix}\right.\)
\(\left(x_1-x_2\right)\left(x_1+x_2\right)=15\Leftrightarrow x_1-x_2=5\)
Kết hợp hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1-x_2=5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=4\\x_2=-1\end{matrix}\right.\)
\(x_1x_2=k-1\Rightarrow k-1=-4\Rightarrow k=-3\)
Thầy giúp em bài này với ạ
tìm x,y nguyên thỏa mãn x^2+y^2+5x^2y^2+60=37xy

Bổ sung thêm điều kiện đề với \(m\ne1\) nữa nhé: )
Nhẩm nghiệm: \(a-b+c=0\) \(\left(m-1-m-1+2=0\right)\)
\(\Rightarrow\) PT có 2 nghiệm \(x_1=-1;x_2=\dfrac{2}{m-1}\)
Nếu \(x_1^2-x_2^2=3\):
\(\left(-1\right)^2-\left(\dfrac{2}{m-1}\right)^2=3\)
=> Không có giá trị m thỏa mãn.
Nếu \(x_1^2-x_2^2=-3\):
\(\left(-1\right)^2-\left(\dfrac{2}{m-1}\right)^2=-3\\ \Rightarrow m=2\left(TM\right)\)

Lời giải:
$\Delta'=4+m^2+1=5+m^2>0$ với mọi $m\in\mathbb{R}$ nên pt luôn có 2 nghiệm phân biệt với mọi $m\in\mathbb{R}$
Áp dụng định lý Viet: \(\left\{\begin{matrix} x_1+x_2=-4\\ x_1x_2=-(m^2+1)\end{matrix}\right.\)
Khi đó:
\(\frac{x_1}{x_2}+\frac{x_2}{x_1}=\frac{-5}{2}\Leftrightarrow \frac{x_1^2+x_2^2}{x_1x_2}=-\frac{5}{2}\)
\(\Leftrightarrow \frac{(x_1+x_2)^2-2x_1x_2}{x_1x_2}=\frac{-5}{2}\Leftrightarrow \frac{(x_1+x_2)^2}{x_1x_2}=-\frac{1}{2}\)
\(\Leftrightarrow \frac{16}{-(m^2+1)}=\frac{-1}{2}\Leftrightarrow m^2+1=32\)
\(\Rightarrow m=\pm \sqrt{31}\)

PT có 2 nghiệm `<=> \Delta' >0 <=> 2^2-1.(m+1)>0<=> m<3`
Viet: `x_1+x_2=-4`
`x_1 x_2=m+1`
`(x_1)/(x_2)+(x_2)/(x_1)=10/3`
`<=> (x_1^2+x_2^2)/(x_1x_2)=10/3`
`<=> ((x_1+x_2)^2-2x_1x_2)/(x_1x_2)=10/3`
`<=> (4^2-2(m+1))/(m+1)=10/3`
`<=> m=2` (TM)
Vậy `m=2`.