Giá trị rút gọn của 20.415.910 - 4.321.810/10.210.620 - 231.277 là
(/ là thay cho phân số)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Phân thức 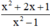 xác định
xác định
⇔ x2 – 1 ≠ 0
⇔ (x – 1)(x + 1) ≠ 0
⇔ x – 1 ≠ 0 và x + 1 ≠ 0
⇔ x ≠ ±1
Vậy phân thức xác định với mọi x ≠ ±1
b) Với x ≠ ±1, ta có:
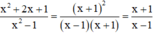
c) + Với x = 2, bạn Thắng tính giá trị biểu thức đúng.
+ Với x = -1, phân thức 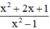 không xác định nên không thể tính giá trị biểu thức nên bạn Thắng tính sai.
không xác định nên không thể tính giá trị biểu thức nên bạn Thắng tính sai.
+ Để tính giá trị của phân thức bằng cách tính giá trị của phân thức rút gọn, ta phải đảm bảo giá trị của biến thỏa mãn điều kiện xác định.

B1:Tổng của tử và mẫu của một phân số là 4120. Sau khi rút gọn được phân số=9/11.phân số chưa rút gọn bằng\(\frac{1854}{2266}\)
B2:Đ/s:\(\frac{33}{39}\)

\(\dfrac{9}{11}\) = \(\dfrac{36}{44}\)⇒ tỉ số tử số lúc đầu so với mẫu số lúc đầu là: \(\dfrac{36}{44}\)
\(\dfrac{5}{4}\) = \(\dfrac{55}{44}\) ⇒ tỉ số tử số lúc sau so với mẫu số lúc đầu là: \(\dfrac{55}{44}\)
Tỉ số của tử số lúc đầu so với tử số lúc sau là : \(\dfrac{36}{44}\) : \(\dfrac{55}{44}\) = \(\dfrac{36}{55}\)
Hiệu tử số lúc sau và tử số lúc đầu là 38
Tử số lúc đầu là: 38 : ( 55 - 36) \(\times\) 36 = 72
Mẫu số lúc đầu là: 72 : \(\dfrac{9}{11}\) = 88
Phân số cần tìm là \(\dfrac{72}{88}\)
Thử lại ta có \(\dfrac{72}{88}\) = \(\dfrac{9}{11}\) ( ok)
\(\dfrac{72+38}{88}\)= \(\dfrac{5}{4}\) ( ok nốt nhá em)
Vậy phân số \(\dfrac{72}{88}\) là phân số cần tìm

a. Ta có \(63=3^2.7\) có 2 ước nguyên tố là 3 và 7
Do \(3n+1\) ko chia hết cho 3 với mọi n tự nhiên
\(\Rightarrow\) Phân số đã cho rút gọn được khi \(3n+1\) và 63 có ước chung là 7
\(\Rightarrow3n+1⋮7\)
Mà 3n+1 và 7 đều chia 3 dư 1 \(\Rightarrow3n+1=7\left(3k+1\right)\Rightarrow n=7k+2\) với k là số tự nhiên
Vậy \(n=7k+2\) với k là số tự nhiên thì phân số đã cho rút gọn được
b.
A là số tự nhiên khi \(63⋮3n+1\Rightarrow3n+1=Ư\left(63\right)\)
Mà \(3n+1⋮̸3\Rightarrow\left[{}\begin{matrix}3n+1=7\\3n+1=1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}n=2\\n=0\end{matrix}\right.\)

b: Theo đề, ta có:
\(\dfrac{a}{74-a}=\dfrac{23}{51}\)
\(\Leftrightarrow51a=1702-23a\)
\(\Leftrightarrow74a=1702\)
hay a=23

Theo đề bài, để A rút gọn được thì 63 phải chia hết cho 3n + 1.
Ư(63) = { 1; 3; 7; 9; 21; 63; -1; -3; -7; -9; -21; -63 }
Với n là số tự nhiên thì mẫu số cũng là số tự nhiên nên loại -1; -3; -7; -9; -21; -63.
Hơn nữa, 3n + 1 chia 3 luôn dư 1 nên loại 3; 9; 21; 63.
Vậy mẫu số cần tìm có thể là 1 hoặc 7.
Nếu mẫu số bằng 1:
3n + 1 = 1
3n + 1 - 1 = 1 - 1
3n = 0
3n / 3 = 0 / 3
n = 0
Nếu mẫu số bằng 7 :
3n + 1 = 7
3n + 1 - 1 = 7 - 1
3n = 6
3n / 3 = 6 / 3
n = 2
Vậy với n = 0 hoặc n = 2 thì A rút gọn được.