Gía trị lớn nhất của x thỏa mãn x3 - 19x- 30= 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 5 2018
Đáp án A
Ta có
S = x 3 y 3 − x 3 + y 3 + 1 = x 3 y 3 − x + y − 3 x y x + y + 1 x y 3 + 12 x y − 63 → t = x y f t = t 3 + 12 t − 63 D o x+y ≥ 2 x y ⇒ x y ≤ 4 ⇒ t ≤ 4 ⇒ M ax 0 ≤ t ≤ 4 f t = f 4 = 49
CM
11 tháng 11 2018
Ta có y= 3-x≥ 1 nên x≤ 2 do đó : x
Khi đó P= x3+ 2( 3-x) 2+ 3x2+4x( 3-x) -5x= x3+x2-5x+18
Xét hàm số f(x) = x3+x2-5x+18 trên đoạn [0 ; 2] ta có:
f ' ( x ) = 3 x 2 + 2 x - 5 ⇒ f ' ( x ) = 0 x ∈ ( 0 ; 2 ) ⇔
F(0) =18; f(1) = 15; f(2) =20
Vậy giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P lần lượt bằng 20 và 15.
Chọn B.
CM
1 tháng 12 2018
Đáp án C
Ta có x + y = 3 ⇒ y = 3 − x ≥ 1 ⇔ x ≤ 2 ⇒ x ∈ 0 ; 2
Khi đó P = f x = x 3 + 2 3 − x 2 + 3 x 2 + 4 x 3 − x − 5 x = x 3 + x 2 − 5 x + 18
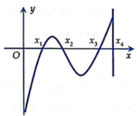
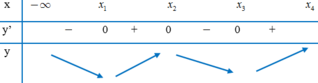
Xét hàm số f x = x 3 + x 2 − 5 x + 18 trên đoạn 0 ; 2 , có f ' x = 3 x 2 + 2 x − 5
Phương trình 0 ≤ x ≤ 2 3 x 2 + 2 x − 5 = 0 ⇔ x = 1. Tính f 0 = 18 , f 1 = 15 , f 2 = 20
Vậy min 0 ; 2 f x = 15 , m a x 0 ; 2 f x = 20 hay P m a x = 20 và P min = 15
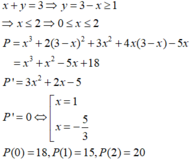
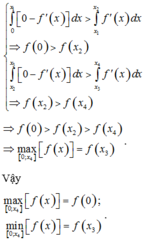
\(x^3-19x-30=0\)
\(\Rightarrow x^3-25x+6x-30=0\)
\(\Rightarrow x\left(x^2-25\right)+6\left(x-5\right)=0\)
\(\Rightarrow x\left(x^2-5^2\right)+6\left(x-5\right)=0\)
\(\Rightarrow x\left(x-5\right)\left(x+5\right)+6\left(x-5\right)=0\)
\(\Rightarrow\left(x-5\right)[x\left(x+5\right)+6]=0\)
\(\Rightarrow\left(x-5\right)\left(x^2+5x+6\right)=0\)
\(\Rightarrow\left(x-5\right)\left(x^2+2x+3x+6\right)=0\)
\(\Rightarrow\left(x-5\right)[x\left(x+2\right)+3\left(x+2\right)]=0\)
\(\Rightarrow\left(x+2\right)\left(x+3\right)\left(x-5\right)=0\)
Trường hợp 1: \(x+2=0\Rightarrow x=-2\)
Trường hợp 2: \(x+3=0\Rightarrow x=-3\)
Trường hợp 3: \(x-5=0\Rightarrow x=5\)
Vậy giá trị lớn nhất của \(x=5\)
\(x^3-19x-30=0\)
\(\Leftrightarrow x^3-5x^2+5x^2-25x+6x-30=0\)
\(\Leftrightarrow\left(x-5\right)\left(x^2+5x+6\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x^2+3x+2x+6\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+3\right)\left(x+2\right)=0\)
\(\Leftrightarrow x-5=0\)hoặc \(x+3=0\)hoặc \(x+2=0\)
\(\Leftrightarrow x=5\)hoặc \(x=-3\)hoặc \(x=-2\).
Vậy \(x=5\)là giá trị thỏa mãn ycbt.