cho tam giác abc cân ở a (a<90 độ) . Từ b và c theo thứ tự kẻ bd vuông góc với ac (d€ac) ce vuông góc với ab (e€ab) .Gọi o là giao điểm của bd và ce. a) chứng minh tam giac abd= tam giac ace.b) chung minh tam giac obc cân.c) kẻ eh là tia phân giác beo(h€bo).dk là phân giác cua cdo(k€co).chứng minh eh=dk.d)gọi i là giao điểm của eh và dk .chứng minh ba điểm a,o,i thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 7 2019
Bài 1 : Hình tự vẽ
a ) Ta có : BM = AB ( theo đề bài )
=> Tam giác AMB cân tại B
b ) Do tam giác ABC vuông cân tại A => AB = AC
mà CN = AB => CN cũng = AC
=> Tam giác ANC cân tại C
c ) Tam giác j cân tại A ???
Bài 2 : Hình bn tự vẽ nhé
a ) AH \(\perp\)BC => \(\Delta AHB\)và \(\Delta AHC\)là hai tam giác vuông
Do tam giác ABC cân tại A => AB = AC và \(\widehat{ABC}=\widehat{ACB}\)
Xét hai tam giác vuông : \(\Delta AHB\)và \(\Delta AHC\)có :
AB = AC ( cmt )
\(\widehat{ABC}=\widehat{ACB}\)( cmt )
nên tam giác AHB = tam giác AHC ( cạnh huyền - góc nhọn )
b ) Do tam giác AHB = tam giác AHC => HB = HC ( hai cạnh tương ứng )
c ) Do tam giác AHB = tam giác AHC => \(\widehat{BAH}=\widehat{CAH}\)
=> AH là tia p/g của \(\widehat{BAC}\)
S
28 tháng 7 2023
Bài 4:
a) Ta có tam giác ABC vuông cân tại A, nên góc BAC = 45 độ. Vì tam giác ACE vuông cân tại E, nên góc CAE = 45 độ. Từ đó suy ra góc CAE + góc BAC = 90 độ, tức là EC vuông góc với BC.
b) Vì tam giác ABC vuông cân tại A, nên góc BAC = 45 độ. Vì tam giác ACE vuông cân tại E, nên góc CAE = 45 độ. Từ đó suy ra góc BAE = góc BAC + góc CAE = 45 độ + 45 độ = 90 độ. Do đó, tứ giác ABCE là tứ giác vuông.
Bài 5:
a) Gọi K là giao điểm của đường thẳng AM và BH. Ta cần chứng minh góc BAK = góc CAK.
Vì CM = CA, ta có góc CMA = góc CAM. Vì đường thẳng AM song song với CA, nên góc CMA = góc KAB (do AB cắt đường thẳng AM tại I). Từ đó suy ra góc CAM = góc KAB.
Vì AH là đường cao, nên góc BAH = góc CAH. Từ đó suy ra góc BAK = góc CAK.
Vậy, AM là phân giác của góc BAH.
b) Ta có AB + AC = AB + AH + HC = BH + HC > BC (theo bất đẳng thức tam giác).
Vậy, luôn luôn có AB + AC < AH + BC.
23 tháng 1 2022
Ta có: \(\widehat{ADB}+\widehat{ADC}=180^o\) (2 góc kề bù)
Mà \(\widehat{ADC}=150^o\)
\(\Rightarrow\widehat{ADB}=30^o\)
CM
29 tháng 4 2018
Vì ΔABC vuông cân tại A nên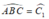 
Lại có: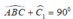 
( tính chất tam giác vuông).
Suy ra: ∠ C 1 = 45 0
Vì
∆
BCD vuông cân tại B nên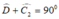 
Lại có: 
( tính chất tam giác vuông).
Suy ra: ∠ C 2 = 45 0
∠ (ACD) = ∠ C 1 + ∠ C 2 = 45 0 + 45 0 = 90 0
⇒ AC ⊥ CD
Mà AC ⊥ AB (gt)
Suy ra: AB //CD
Vậy tứ giác ABCD là hình thang vuông.
2 tháng 9 2023
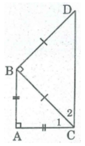
ΔBDC vuông cân tại B
=>góc BCD=góc BDC=45 độ
ΔABC vuông cân tại A
=>góc ABC=góc ACB=45 độ
góc ABC=góc DCB
mà hai góc này ở vị trí so le trong
nên AB//DC
mà AB vuông góc AC
nên DC vuông góc AC
Xét tứ giác ABDC có
AB//DC
góc CAB=90 độ
Do đó: ABDC là hình thang vuông
11 tháng 7 2019
a) Ta có : ACB = 45° ( ∆ABC vuông cân tại A )
Ta có : AEC = 45° ( ∆ACE vuông cân tại E )
=> ACB = AEC = 45°
Mà 2 góc này ở vị trí so le trong
=> AE//BC
=> AEBC là hình thang
Mà AEC = 90°
=> AEBC là hình thang vuông
PL
21 tháng 6 2016
Vì tam giác ABC vuông cân tại A (gt) nên góc ABC = góc ACB = 90 : 2 = 45 độ
Vì tam giác BCD vuông cân tại B (gt) nên góc BDC = góc BCD = 90 : 2 = 45 độ
Ta có: góc ACB + góc BCD = góc ACD = 45 độ + 45 độ = 90 độ
hay AC vuông góc DC. (1)
Vì tam giác ABC vuông cân tại A (gt) nên AC vuông góc AB (2)
Từ (1) và (2) suy ra DC // AB
Do đó tứ giác ABCD là hình thang.
cm ao và oi cùng đi qua một đường thẳng