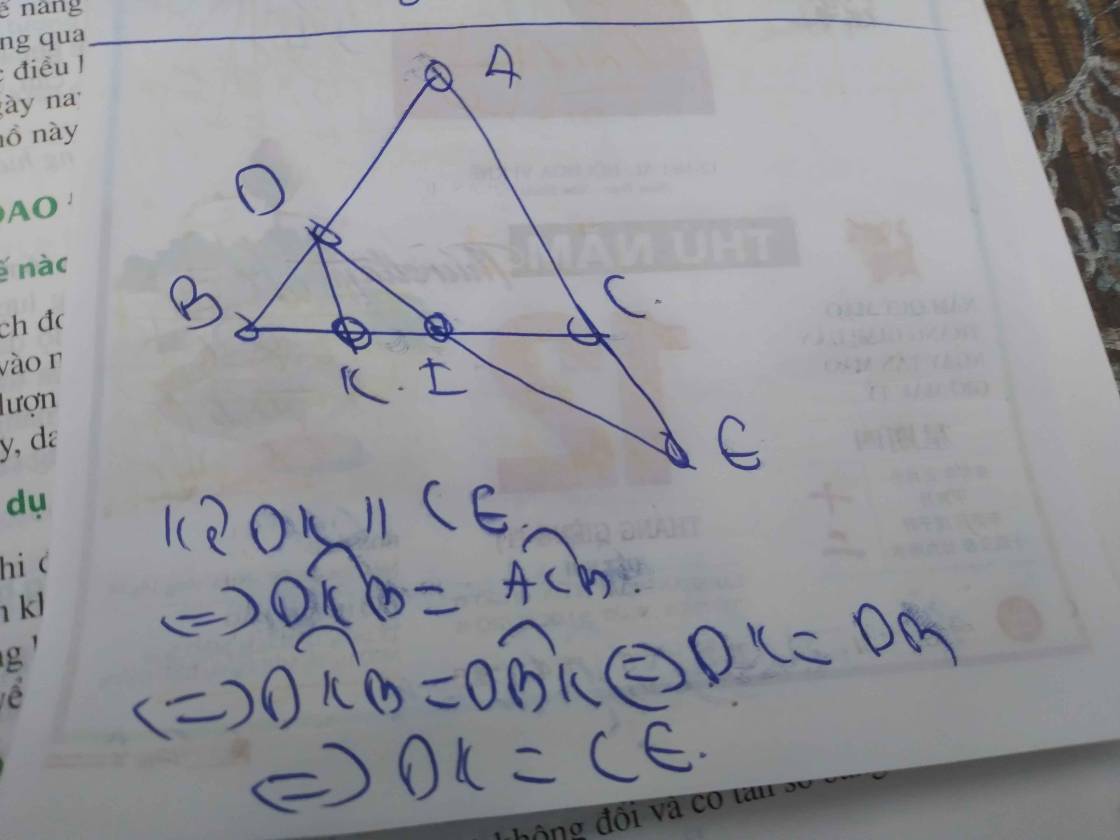
cho tam giác abc có ab=ac. trên tia đối của tia ba lấy điểm d và trên tia đối của tia ca lấy điểm e sao cho bd=ce. CMR:
a)BE=Ce
b)DI=IE
c)AI vông góc với BC
d)BC//DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

19 tháng 12 2018
a) Chứng minh rằng: BE=CD
Xét tam giác ADC và tam giác AEB, ta có
- AC = AB (đề bài cho)
- góc A chung
- AD = AB + BD, và AE = AC + CE. Mà AB = AC, BD = CE, nên AD = AE
==> tam giác ADC = tam giác AEB (cạnh - góc - cạnh)
==> BE = CD (đpcm)
2,3) mình có việc nên ko ghi ra bây giờ được

CM
16 tháng 2 2019
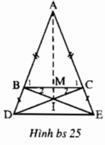
Các tam giác cân ABC và ADC có chung góc ở đỉnh ∠A nên ∠B1 = ∠ADE. Mà hai góc này ở vị trí đồng vị nên suy ra BC // DE.

13 tháng 1 2022
a: Xét ΔBAD và ΔBKD có
BA=BK
\(\widehat{ABD}=\widehat{KBD}\)
BD chung
Do đó: ΔBAD=ΔBKD
Suy ra: \(\widehat{BAD}=\widehat{BKD}=90^0\)
hay DK\(\perp\)BC
b: Xét ΔBEC có BE=BC
nên ΔBEC cân tại B
mà BI là đường phân giác
nên BI là đường cao