Cho hàm số y=2x-3/x-2 có đồ thị hàm số (C) và hai đường thẳng d1: x=2, d2: y=2. Tiếp tuyến bất kì của (C) cắt d1 và d2 lần lượt tại A và B. Khi AB có độ dài nhỏ nhất thì tổng các hoành độ tiếp điểm bằng?
Mọi người giúp em với ạ. Em cảm ơn ạ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 3 2018
Đáp án C.
Ta có:
g x = x . f 2 x − 1 ⇒ g ' x = f 2 x − 1 + 2 x . f ' 2 x − 1
Suy ra g ' 1 = f 1 + 2 f ' 1 mà d 1 vuông góc với d 2 ⇒ f ' 1 . g ' 1 = − 1
⇔ f ' 1 . f 1 + 2 f ' 1 = − 1 ⇔ 2. f ' 1 2 + f 1 + 1 = 0 ( * )
Phương trình (*) có nghiệm khi và chỉ khi:
Δ = f 1 2 − 4.2 ≥ 0 ⇔ f 1 ≥ 2 2 .
CM
23 tháng 10 2017
Chọn đáp án C
Ta có
Đường thẳng d 1 là tiếp tuyến của đồ thị hàm số y = f x tại điểm x = 1 nên có hệ số góc là k 1 = f ' 1
Đường thẳng d 2 là tiếp tuyến của đồ thị hàm y = g x = x . f 2 x - 1 tại điểm x = 1 nên có hệ số góc là
k 2 = g ' 1 = f 1 + 2 f ' 1
Mà d 1 ⊥ d 2 nên
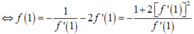
Do f ' 1 ≠ 0 nên
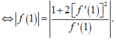
Đặt f ' 1 = t t ≠ 0
Xét hàm số f t = 1 + 2 t 2 t
* Nếu t > 0 thì
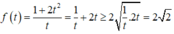
* Nếu t < 0 thì
Vậy h t ≤ 2 2 , ∀ t ≠ 0 hay f 1 ≥ 2 2
CM
3 tháng 1 2019
Ta có phương trình hoành độ giao điểm của d 1 v à d 2 : m x – 2 = 1 2 x + 1 ( * )
Để hai đường thẳng d 1 v à d 2 cắt nhau tại một điểm có hoành độ x = − 4 t h ì x = − 4 thỏa mãn phương trình (*)
Suy ra m . ( − 4 ) – 2 = 1 2 . ( − 4 ) + 1 ⇔ − 4 m – 2 = − 2 + 1 ⇔ − 4 m = 1 ⇔ m = 1 4
Đáp án cần chọn là: A
CM
10 tháng 10 2018
Ta có phương trình hoành độ giao điểm của d 1 v à d 2 : m 2 x + 1 = 3 x − 2 ( * )
Để hai đường thẳng d 1 v à d 2 cắt nhau tại một điểm có hoành độ x = − 1 t h ì x = − 1 thỏa mãn phương trình (*)
Suy ra m 2 . ( − 1 ) + 1 = 3 . ( − 1 ) – 2 ⇔ - m 2 + 1 = − 5 ⇔ - m 2 = − 6 ⇔ m = 12
Đáp án cần chọn là: B