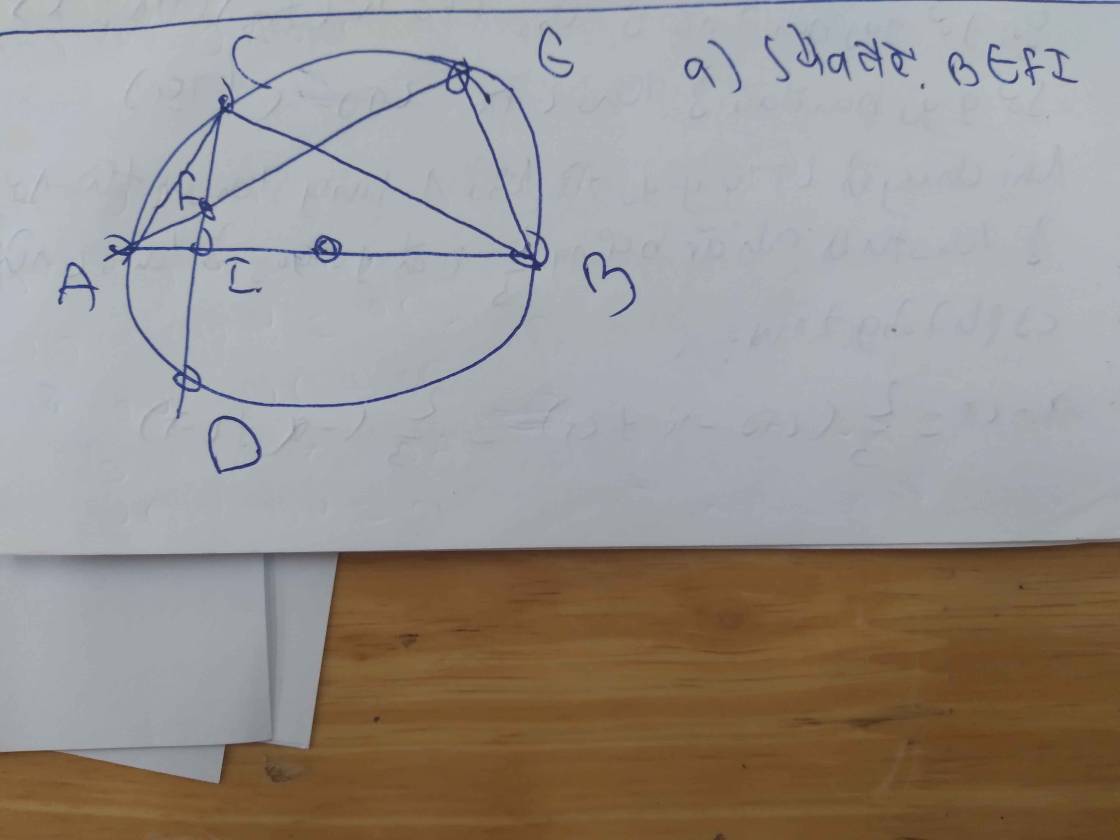
Cho đường tròn tâm O, đường kính AC. Vẽ dây BD vuông góc với AC tại K (K nằm giữa A và O). Lấy điểm E trên cung nhỏ CD (E không trùng C và D), AE cắt BD tại H.a) Cm: tgCBD cân và tg CEHK nội tiếp.b) C...

NH

Ngọc Hân Nguyễn

15 tháng 4 2020 - olm

Cho đường tròn tâm O, đường kính AC. Vẽ dây BD vuông góc với AC tại K (K nằm giữa A và O). Lấy điểm E trên cung nhỏ CD (E không trùng C và D), AE cắt BD tại H.a) Cm: tgCBD cân và tg CEHK nội tiếp.b) Cm: AD2 = AH. AE c) Cho BD = 24cm; BC = 20cm. TÍnh chu vi hình...

Đọc tiếp

#Toán lớp 9

0

TN

ta nguyễn

5 tháng 4 2022

cho đường tròn tâm O đường kính AB. vẽ dây cung CD vuông góc với AB tại I(I nằm giữa A và O). lấy điểm E trên cung nhỏ BC (E khác B và C) AE cắt CD tại F chứng minh:

IA.IB=IC.ID VÀ AE.AF=\(AC^2\)(Biết BEFI đã nội tiếp đường tròn)

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

3 tháng 7 2023

Xét ΔIAC vuông tại I và ΔIDB vuông tại I có

góc IAC=góc IDB

=>ΔIAC đồng dạng với ΔIDB

=>IA/ID=IC/IB

=>IA*IB=ID*IC

Xét ΔACF và ΔAEC có

góc ACF=góc AEC

góc CAF chung

=>ΔACF đồng dạng với ΔAEC

=>AC/AE=AF/AC

=>AC^2=AE*AF

Đúng(0)

AQ

Anh Quynh

21 tháng 1 2022

Cho đường tròn tâm O đường kính AB.Vẽ dây cung CD vuông góc với AB tại I (I nằm giữa A và O).Lấy điểm E trên cung nhỏ BC,E khác B và C,AE cắt CD tại F.
Chứng minh:
a. BEFI là tứ giác nội tiếp đường tròn.
b. AE . AF = AC^2

#Toán lớp 9

1

TH

Thanh Hoàng Thanh

21 tháng 1 2022

a) Xét (O): E \(\in\) (O) (gt).

\(\Rightarrow\) \(\widehat{AEB}=90^o\) (Góc nội tiếp).

Xét tứ giác BEFI:

\(\widehat{AEB}+\widehat{CIB}=90^o+90^o=180^o.\)

Mà 2 góc này ở vị trí đối nhau.

\(\Rightarrow\) BEFI là tứ giác nội tiếp đường tròn.

b) Xét (O): \(CD\perp AB\) tại I (gt).

AB là đường kính; CD là dây (gt).

\(\Rightarrow\) I là trung điểm của CD.

Xét tam giác ACD:

AI là đường trung tuyến (I là trung điểm của CD).

AI là đường cao \(\left(AI\perp CD\right).\)

\(\Rightarrow\) Tam giác ACD cân tại A. \(\Rightarrow\) AC = AD (Tính chất tam giác cân).

Xét (O): AC = AD (cmt). \(\Rightarrow sđ\stackrel\frown{AC}=sđ\stackrel\frown{AD}.\)

Xét (O): \(\widehat{ACF}=\dfrac{1}{2}sđ\stackrel\frown{AD}\) (Góc nội tiếp).

Mà \(sđ\stackrel\frown{AD}=sđ\stackrel\frown{AC}\left(cmt\right).\)

\(\Rightarrow\) \(\widehat{ACF}=\dfrac{1}{2}sđ\stackrel\frown{AC}.\)

Mà \(\widehat{AEC}=\dfrac{1}{2}sđ\stackrel\frown{AC}\) (Góc nội tiếp).

\(\Rightarrow\widehat{ACF}=\widehat{AEC}.\)

Xét tam giác ACF và tam giác AEC:

\(\widehat{A}chung.\)

\(\widehat{ACF}=\widehat{AEC}\left(cmt\right).\)

\(\Rightarrow\) Tam giác ACF \(\sim\) Tam giác AEC (g - g).

\(\Rightarrow\) \(\dfrac{AC}{AE}=\dfrac{AF}{AC}\) (2 cạnh tương ứng tỉ lệ).

\(\Rightarrow AC^2=AE.AF\left(đpcm\right).\)

Đúng(2)

Q

Quang

14 tháng 9 2023

Cho đường tròn tâm O đường kính AB=2R. Vẽ dây cung CD vuông góc với AB tại I(I nằm giữa A và O). Lấy điểm E trên cung nhỏ BC(E khác B và C), AE cắt CD tại Fa) Chứng minh tứ giác BEFL nội tiếp trong một đường trònb) Tính độ dài cạnh AC theo R và góc ACD khi góc BAC=60độc) Chứng minh khi điểm E chạy trên cung nhỏ BC thì tâm đường tròn ngoại tiếp tam giác CEF luôn thuộc một đường thẳng cố...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

16 tháng 10 2023

loading...

Đúng(0)

QT

Quỳnh Thơ Bùi

5 tháng 4 2022

Cho đường tròn tâm O đường kính AB. Dây CD vuông góc với AB tại E (E nằm giữa A và O; E không trùng A, không trùng O). Lấy điểm M thuộc cung nhỏ BC sao cho cung MB nhỏ hơn cung MC. Dây AM cắt CD tại F. Tia BM cắt đường thẳng CD tại K. 1.Chứng minh tứ giác BMFE nội tiếp. 2.Chứng minh BF vuông góc với AK và EK.EF = EA.EB 3.Tiếp tuyến của (O) tại M cắt tia KD tại I. Chứng minh IK =...

Đọc tiếp

#Toán lớp 9

1

XO

Xyz OLM

5 tháng 4 2022

undefined

Đúng(1)

NT

nguyen thi hoa trinh

12 tháng 3 2021

Cho đường tròn tâm O đường kính AB . Gọi H là điểm nằm giữa O và B . Kẻ dây CD vuông góc với AB tại H . Trên cung nhỏ AC lấy điểm E , kẻ CK vuông góc với AE tại K . Đường thẳng DE cắt CK tại F . Chứng minh :a, Tứ giác AHCK nội tiếp đường tròn b, AH . AD = AD^2 c, Tam giác ACF...

Đọc tiếp

#Toán lớp 9

0

CN

Cao Nam Phong

18 tháng 3 2022

Bài 4: Cho đường tròn (O) đường kính AB. Lấy điểm I nằm giữa A và 0, vẽ dây CD vuông góc với AB tại I. a) Lấy E trên cung nhỏ BC (E không trùng lặp B và C) AE cắt CD tại F. Chứng minh: Tứ giác BEFI nội tiếp b ) AI. AB = AF.AE c) Khi E di chuyển trên cung nhỏ BC thì tâm đường tròn ngoại tiếp ACFE luôn thuộc một đường cố...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

22 tháng 1

a: Xét (O) có

ΔAEB nội tiếp

AB là đường kính

Do đó: ΔAEB vuông tại E

Xét tứ giác BEFI có \(\widehat{BEF}+\widehat{BIF}=90^0+90^0=180^0\)

nên BEFI là tứ giác nội tiếp

b: Xét ΔAIF vuông tại I và ΔAEB vuông tại E có

\(\widehat{EAB}\) chung

Do đó: ΔAIF~ΔAEB

=>\(\dfrac{AI}{AE}=\dfrac{AF}{AB}\)

=>\(AI\cdot AB=AF\cdot AE\)

Đúng(0)

MB

Minh Bình

19 tháng 1

Cho (O), đường kính AB. Lấy H nằm giữa O và B, kẻ dây CD vuông góc với AB tại H. Trên cung nhỏ AC lấy E, Kẻ CK vuông góc với AE tại K. DE cắt CK tại F

a) c/m tg AHCK nội tiếp

b) c/m HK//DE

c) c/m AF^2=AH.AB

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

20 tháng 1

a: Xét tứ giác AHCK có \(\widehat{AHC}+\widehat{AKC}=90^0+90^0=180^0\)

nên AHCK là tứ giác nội tiếp

b: ta có: AHCK là tứ giác nội tiếp

=>\(\widehat{CHK}=\widehat{CAK}=\widehat{CAE}\left(1\right)\)

Xét (O) có

\(\widehat{CAE}\) là góc nội tiếp chắn cung CE

\(\widehat{CDE}\) là góc nội tiếp chắn cung CE

Do đó: \(\widehat{CAE}=\widehat{CDE}\left(2\right)\)

Từ (1),(2) suy ra \(\widehat{CHK}=\widehat{CDE}\)

mà hai góc này là hai góc ở vị trí đồng vị

nên HK//DE

Đúng(1)

L

LuKenz

16 tháng 8 2021

Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I ( I nằm giữa A và O ). Lấy điểm E trên cung nhỏ BC (E khác B và C) AE cắt CD tại F . Chứng minh: bốn điểm B E F I thuộc một đường...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

16 tháng 8 2021

Xét (O) có

\(\widehat{AEB}\) là góc nội tiếp chắn nửa đường tròn

nên \(\widehat{AEB}=90^0\)

Xét tứ giác BEFI có

\(\widehat{BEF}+\widehat{FIB}=180^0\)

nên BEFI là tứ giác nội tiếp

hay B,E,F,I cùng thuộc 1 đường tròn

Đúng(0)

HH

Huỳnh Hướng Ân

13 tháng 5 2016 - olm

cho đường tròn tâm O đường kính AB. vẽ dây cung CD vuông góc với AB tại I ( I nằm giữa A và O ). lấy điểm E trên cung nhỏ BC ( E khác B và C), AE cắt CD tại F. chứng minh:

a) BEFI là tứ giác nội tiếp đường tròn

b) AE.AF=AC^2

c) khi E chạy trên cung nhỏ BC thì tâm đường tròn ngoại tiếp tam giác CEF luôn thuộc một đường thẳng cố định.

#Toán lớp 9

1

NT

Nguyễn Thị Hà Vy

13 tháng 5 2016

a, ta có góc FIB=90° (gt) góc FEB= góc AEB=90° (góc ntiêp chắn nửa đg tròn) => góc FIB+FEB=180° => tứ giác BEFI nội tiếp b) Xét tam giác AFC và tam giác ACE có: góc CAE chung Do AO vuông góc vs CD => cung AC=cung AD mà góc ACD=1/2 sđ cung AD; Góc CEA=1/2 sđ Cung AC => góc ACD=CEA (chăn 2 cung =nhau) => tam giác AFC đồng dạng vs tam giác ACE (g.g) => AE/AC=AC/AF => AE.AF=AC^2 (đpcm)

Đúng(0)

T

THN

7 tháng 11 2017 - olm

Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I( I nằm giữa A và O). Lấy điểm E trên cung nhỏ BC( E khác B và C), Ae cắt CD tại F. Chứng minh:

a) BEFI là tứ giác nội tiếp đường tròn.

b) AE.AF = AC².

c) Khi E chạy trên cung nhỏ BC thì tâm đường tròn ngoại tiếp tam giac CEF luôn thuộc đường thẳng cố định.

#Toán lớp 9

3

BB

Băng băng

7 tháng 11 2017

a, Ta có góc FIB=90° (gt) góc FEB= góc AEB=90° (góc ntiêp chắn nửa đg tròn) => góc FIB+FEB=180° => Tứ giác BEFI nội tiếpb) Xét tam giác AFC và tam giác ACE có: góc CAE chung Do AO vuông góc vs CD => cung AC=cung AD mà góc ACD=1/2 sđ cung AD; Góc CEA=1/2 sđ Cung AC => góc ACD=CEA (chăn 2 cung =nhau) => tam giác AFC đồng dạng với tam giác ACE (g.g) => AE/AC=AC/AF => AE.AF=AC^2 (đpcm)c, Có ^ACF = ^CBA (phụ ^ICB) . Trong (O) có ^ACF = ^CEF (chắn hai cung bằng nhau AC và cung AD) vậy ^ACF = ^CEF < 90 nên AC là tiếp tuyến của đường tròn ngoại tiếp tam giác CEF suy ra tâm của đường tròn đường tròn ngoại tiếp tứ giác CEF thuộc đường vuông góc AC tại C nên tâm thuộc AC cố định

Đúng(0)

K

KAl(SO4)2·12H2O

28 tháng 5 2018

a) Tứ giác BEFI có: BFF = 90^o(gt)

BEF = BEA = 90^o

=> Tứ giác BEFI là nội tiếp đường tròn đường kính BF

b)

Vì \(AB\perp CD\)nên AC = AD

=> ACF = AEC

Xét tam giác ACF và tam giác AEC có gốc chung A và ACF = AEC

=> Tam giác ACF song song với tam giác AEC => \(\frac{AC}{AF}=\frac{AB}{AC}\)

=> AE . AF = AC²

c) Theo câu b) ta có: ACF = AEC = > AC là tiếp tuyến của đường tròn ngoại tiếp của tam giác CEF (1)

Mặt khác, ta có: ACB = 90^o(góc nội tiếp chứa đường tròn)

\(\Rightarrow AC\perp CB\)(2)

Từ (1) và (2) => CB chứa đường kính của đường tròn ngoại tiếp tam giác CEF, mà CB cố định nên tâm của đường tròn ngoại tiếp tam giác CEF thuộc CB cố định E thay đổi trên cung nhỏ BC.

Đúng(1)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP