Cho đoạn thẳng AB và O là trung điểm của AB. Trên cùng một nửa mặt phẳng bờ AB vẽ các tia Ax, By vuông góc với AB. Lấy C là điểm bất kỳ thuộc tia Ax khác điểm A. Tia CO cắt tia đối của tia By tại D. Đường vuông góc với CO tại O cắt tia By ở E. Chứng minh rằng:
a) \Delta OAC=\Delta OBDΔOAC=ΔOBD
b) \Delta OCE=\Delta ODEΔOCE=ΔODE
c) CE=AC+BE
AC=\dfrac{1}{2}BCAC=21BC

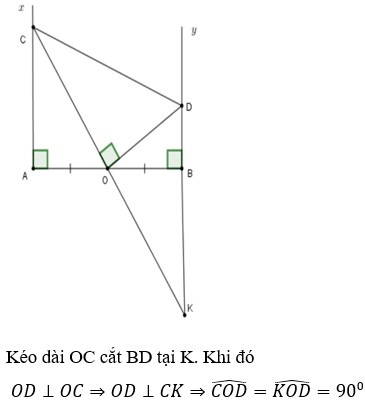





a, Xét △OAC vuông tại A và △OBD vuông tại B
Có: OA = OB (gt)
COA = DOB (2 góc đối đỉnh)
=> △OAC = △OBD (cgv-gnk)
b, Xét △OCE và △ODE cùng vuông tại O
Có: OE là cạnh chung
OC = OD (△OAC = △OBD)
=> △OCE = △ODE (2cgv)
c, Ta có: DE = BE + BD mà BD = AC (△OBD = △OAC) ; CE = DE (△OCE = △ODE)
=> CE = BE + AC (đpcm)
ý AC = 1/2 BC còn có điều kiện gì nữa ko??