giải hộ mình với
Câu 1. Trong mặt phẳng tọa độ, cho đường thẳng d: (x+2)/(-1)=(y-3)/(4)
a/. Tìm một điểm có tọa độ xác định, một VTCP, một VTPT của đường thẳng d
b/.Viết phương trình tham số của đường thẳng d. Tìm hệ số góc của đường thẳng d
Câu 2 viết phương trình đường thẳng ∆ theo đoạn chắn, biết ∆ đi qua A(0;-6),B(2;0)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi (d): y=ax+b
Vì (d)//y=2x-3 nên \(\left\{{}\begin{matrix}a=2\\b\ne-3\end{matrix}\right.\)
Vậy: (d): y=2x+b
Vì (d) đi qua điểm C(-1;4) nên
Thay x=-1 và y=4 vào (d), ta được:
\(2\cdot\left(-1\right)+b=4\)
hay b=6
Vậy: (d): y=2x+6
Thay y=0 vào (d), ta được:
2x+6=0
hay x=-3
Vậy: A(-3;0)
b) Vì y=ax+b đi qua hai điểm B(4;0) và C(-1;4) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}4a+b=0\\-a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5a=-4\\b=a+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{4}{5}\\b=\dfrac{-4}{5}+4=\dfrac{-4}{5}+\dfrac{20}{5}=\dfrac{16}{5}\end{matrix}\right.\)

a) Gọi (d): y=ax+b
Vì (d)//y=2x-3 nên ta có: \(\left\{{}\begin{matrix}a=2\\b\ne-3\end{matrix}\right.\)
=> (d): y=2x+b
Thay x=-1 và y=4 vào (d), ta được:
\(2\cdot\left(-1\right)+b=4\)
\(\Leftrightarrow b=6\)
Vậy: (D): y=2x+6
Thay y=0 vào (d),ta được:
\(2x+6=0\)
\(\Leftrightarrow x=-3\)
Vậy: A(-3;0)
b) Vì đồ thị hàm số y=ax+b đi qua hai điểm B(4;0) và C(-1;4) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}4a+b=0\\-a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5a=-4\\-a+b=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{4}{5}\\b=4+a=4+\dfrac{-4}{5}=4-\dfrac{4}{5}=\dfrac{16}{5}\end{matrix}\right.\)
Vậy: \(a=-\dfrac{4}{5}\); \(b=\dfrac{16}{5}\)
c) Độ dài đoạn thẳng AB là:
\(AB=\sqrt{\left(-3-4\right)^2+\left(0-0\right)^2}=7\)(cm)
Độ dài đoạn thẳng AC là:
\(AC=\sqrt{\left(-3+1\right)^2+\left(0-4\right)^2}=2\sqrt{5}\left(cm\right)\)
Độ dài đoạn thẳng BC là:
\(BC=\sqrt{\left(4+1\right)^2+\left(0-4\right)^2}=\sqrt{41}\left(cm\right)\)
Chu vi tam giác ABC là:
\(C_{ABC}=AB+AC+BC\)
\(=7+2\sqrt{5}+\sqrt{41}\)
\(\simeq17,9\left(cm\right)\)
Còn thiếu tính góc tạo bởi đường thẳng BC và trục Ox mà bạn

Bài 3:
Đặt \(a=m^2-4\)
\(a)\) Đồ thị hàm số \(y=\left(m^2-4\right)x-5\)nghịch biến
\(\Leftrightarrow a< 0\)
\(\Leftrightarrow m^2-4< 0\)
\(\Leftrightarrow m^2< 4\)
\(\Leftrightarrow-\sqrt{4}< m< \sqrt{4}\)
\(\Leftrightarrow-2< m< 2\)
Vậy với \(-2< m< 2\)thì hàm số nghịch biến
\(b)\) Đồ thị hàm số \(y=\left(m^2-4\right)x-5\)đồng biến \(\forall x>0\)
\(\Leftrightarrow a>0\)
\(\Leftrightarrow m^2-4>0\)
\(\Leftrightarrow m^2>4\)
\(\Leftrightarrow\orbr{\begin{cases}m>2\\m< -2\end{cases}}\)
Vậy với \(\orbr{\begin{cases}m>2\\m< -2\end{cases}}\)thì hàm số đồng biến \(\forall x>0\)

a) Thay tọa dộ của điểm T vào dg thẳng d ta dc: -2.(-2) - 6 = -2 (Thỏa mãn)
Vậy điểm T có thuộc dg thẳng d
b) Pt hoành độ giao điểm của (d) và (P) là: -8x2 = -2x - 6
<=> 8x2 - 2x - 6 = 0
<=> (x - 1)(8x + 6) = 0 <=> \(\orbr{\begin{cases}x=1\\x=-\frac{3}{4}\end{cases}}\)
* Với x = 1 => y = -8
* Với x = -3/4 => y = -9/2
Tự kết luận nha

a: 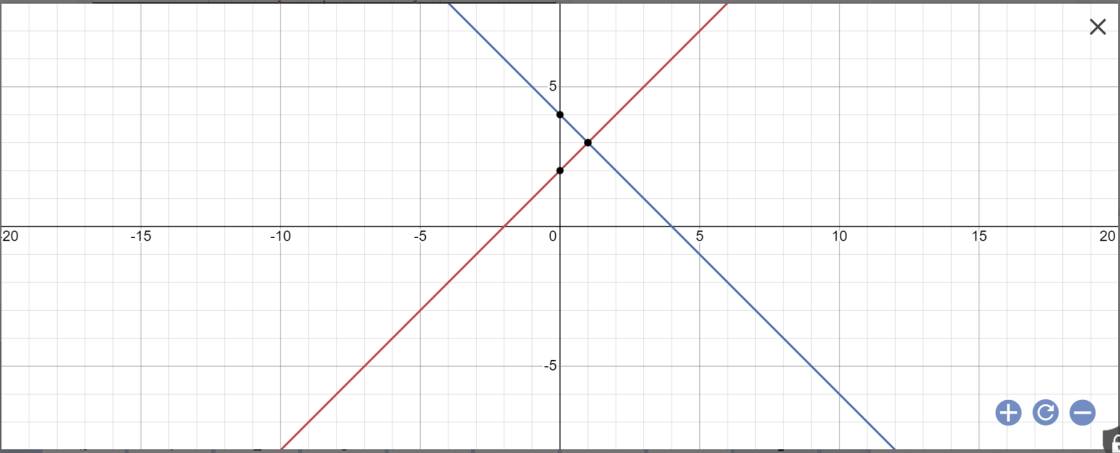
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}x+2=-x+4\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=2\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1+2=3\end{matrix}\right.\)
Thay x=1 và y=3 vào (d3), ta được:
\(1\cdot m+m=3\)
=>2m=3
=>\(m=\dfrac{3}{2}\)

b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)
hay \(-x-4=3x+2\)
\(\Leftrightarrow-x-4-3x-2=0\)
\(\Leftrightarrow-4x-6=0\)
\(\Leftrightarrow-4x=6\)
hay \(x=-\dfrac{3}{2}\)
Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được:
\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)
Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)
c) Vì (D2) song song với (D) nên a=-1
hay (D2): y=-x+b
Vì (D2) đi qua điểm B(-2;5)
nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được:
-(-2)+b=5
hay b=5-2=3
Vậy: (D2): y=-x+3
b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)
hay \(-x-4=3x+2\)
\(\Leftrightarrow-x-4-3x-2=0\)
\(\Leftrightarrow-4x-6=0\)
\(\Leftrightarrow-4x=6\)
hay \(x=-\dfrac{3}{2}\)
Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được:
\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)
Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)
c) Vì (D2) song song với (D) nên a=-1
hay (D2): y=-x+b
Vì (D2) đi qua điểm B(-2;5)
nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được:
-(-2)+b=5
hay b=5-2=3
Vậy: (D2): y=-x+3

a:
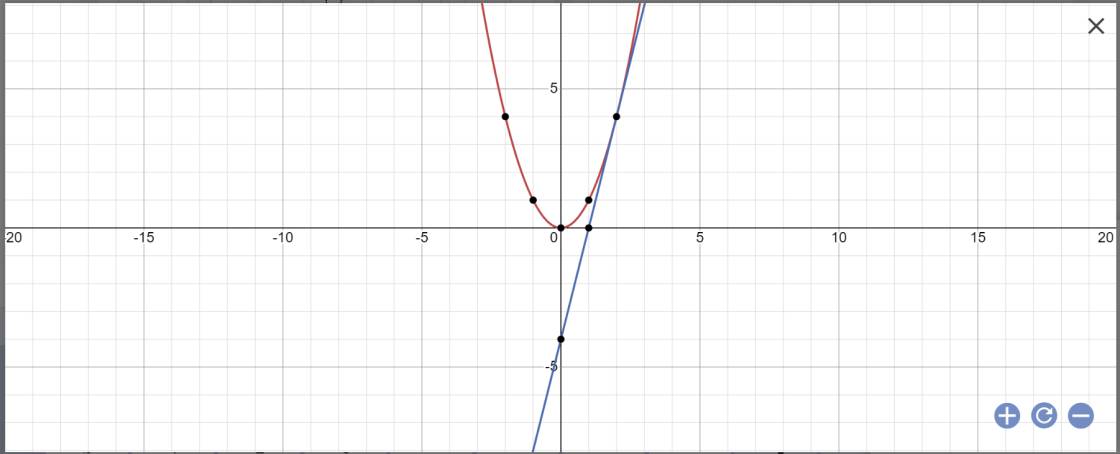
b: PTHĐGĐ là:
2x^2-(2m-2)x+m-1=0
Δ=(2m-2)^2-4*2*(m-1)
=4m^2-8m+4-8m+8
=4m^2-16m+12
=4m^2-2*2m*4+16-4=(2m-4)^2-4=(2m-6)(2m-2)
Để (d) cắt (P) tại 2 điểm pb thì (2m-6)(2m-2)>0
=>m>3 hoặc m<1
Đường thẳng d có phương trình dạng chính tắc: \(\frac{x+2}{-1}=\frac{y-3}{4}\)
\(\Rightarrow\) d đi qua điểm \(M\left(-2;3\right)\)
d nhận \(\left(-1;4\right)\) là 1 vtcp
\(\Rightarrow\) d nhận \(\left(4;1\right)\) là 1 vtpt
b/ Phương trình tham số d: \(\left\{{}\begin{matrix}x=-2-t\\y=3+4t\end{matrix}\right.\)
Hệ số góc: \(k=\frac{4}{-1}=-4\)
Câu 2:
Phương trình đoạn chắn của \(\Delta\): \(\frac{x}{2}+\frac{y}{-6}=1\)