Question

[Nguyễn Minh Đức]

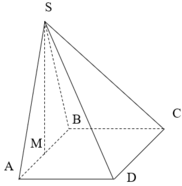
Cho hình chóp S.ABCD, đáy là hình vuông cạnh a. Mặt bên SAB là tam giác đều; SCD là tam giác vuông tại S. Gọi I,J là trung điểm AB và CD.

a, Tính các cạnh của tam giác SIJ và chứng minh \(SI\perp\left(SCD\right),SJ\perp\left(SAB\right)\)

b, Gọi H là hình chiếu của S trên IJ. Chứng minh \(SH\perp AC\)

Answer 1

[Nguyễn Việt Lâm]

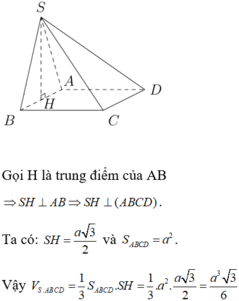
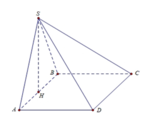
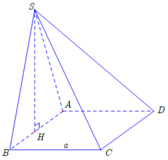
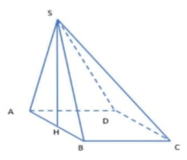
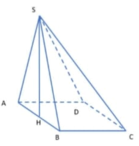
Gọi H là hình chiếu vuông góc của S lên (ABCD) \(\Rightarrow H\) thuộc trung trực AB (do SAB đều)

\(\Rightarrow H\) thuộc trung trực CD \(\Rightarrow HC=HD\Rightarrow SC=SD\Rightarrow\Delta SCD\) vuông cân tại S (1)

\(\Rightarrow SC=SD=\frac{a\sqrt{2}}{2}\)

\(IJ=AB=a\) ; \(SI=\frac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)

\(SJ=\frac{CD}{2}=\frac{a}{2}\) (trung tuyến ứng với cạnh huyền tam giác vuông)

\(\Rightarrow IJ^2=SJ^2+SI^2\Rightarrow SI\perp SJ\) (pitago đảo)

Mà \(CD\perp\left(SIJ\right)\Rightarrow CD\perp SI\)

\(\Rightarrow SI\perp\left(SCD\right)\)

Tương tự \(AB\perp\left(SIJ\right)\Rightarrow AB\perp SJ\Rightarrow SJ\perp\left(SAB\right)\)

b/ (1) \(\Rightarrow SH\perp\left(ABCD\right)\Rightarrow SH\perp AC\)