Tìm GTNN của F=(mx+2y-2m)2+(x+y-2)2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 1 2024
1: Để hệ có nghiệm duy nhất thì \(\dfrac{1}{m}\ne\dfrac{1}{-1}=-1\)
=>\(m\ne-1\)
2: \(\left\{{}\begin{matrix}x+y=1\\mx-y=2m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+y+mx-y=1+2m\\x+y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\left(m+1\right)=2m+1\\x+y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{2m+1}{m+1}\\y=1-x=1-\dfrac{2m+1}{m+1}=\dfrac{m+1-2m-1}{m+1}=-\dfrac{m}{m+1}\end{matrix}\right.\)
x+2y=2
=>\(\dfrac{2m+1}{m+1}+\dfrac{-2m}{m+1}=2\)
=>\(\dfrac{1}{m+1}=2\)
=>\(m+1=\dfrac{1}{2}\)
=>\(m=-\dfrac{1}{2}\left(nhận\right)\)
AA
1
TT
16 tháng 1 2021
\(F=2x^2+y^2+2y\left(x+1\right)+\left(x+1\right)^2-x^2-2x-1-2x+2\)
\(=\left(y+x+1\right)^2+x^2-4x+1\)
\(=\left(x+y+1\right)^2+\left(x-2\right)^2-3\ge-3\forall x;y\)
=> \(MinF=-3\Leftrightarrow\left\{{}\begin{matrix}x+y+1=0\\x-2=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-3\end{matrix}\right.\)
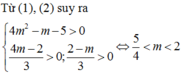
- Với \(m=2\Rightarrow F=5\left(x+y-2\right)^2\ge0\)
\(F_{min}=0\) khi \(x+y=2\)
- Với \(m\ne2\)
\(\left\{{}\begin{matrix}\left(mx+2y-2m\right)^2\ge0\\\left(x+y-2\right)^2\ge0\end{matrix}\right.\) \(\Rightarrow F_{min}=0\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}mx+2y=2m\\x+y=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}mx+2y=2m\\2x+2y=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(m-2\right)x=2\left(m-2\right)\\y=2-x\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)