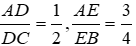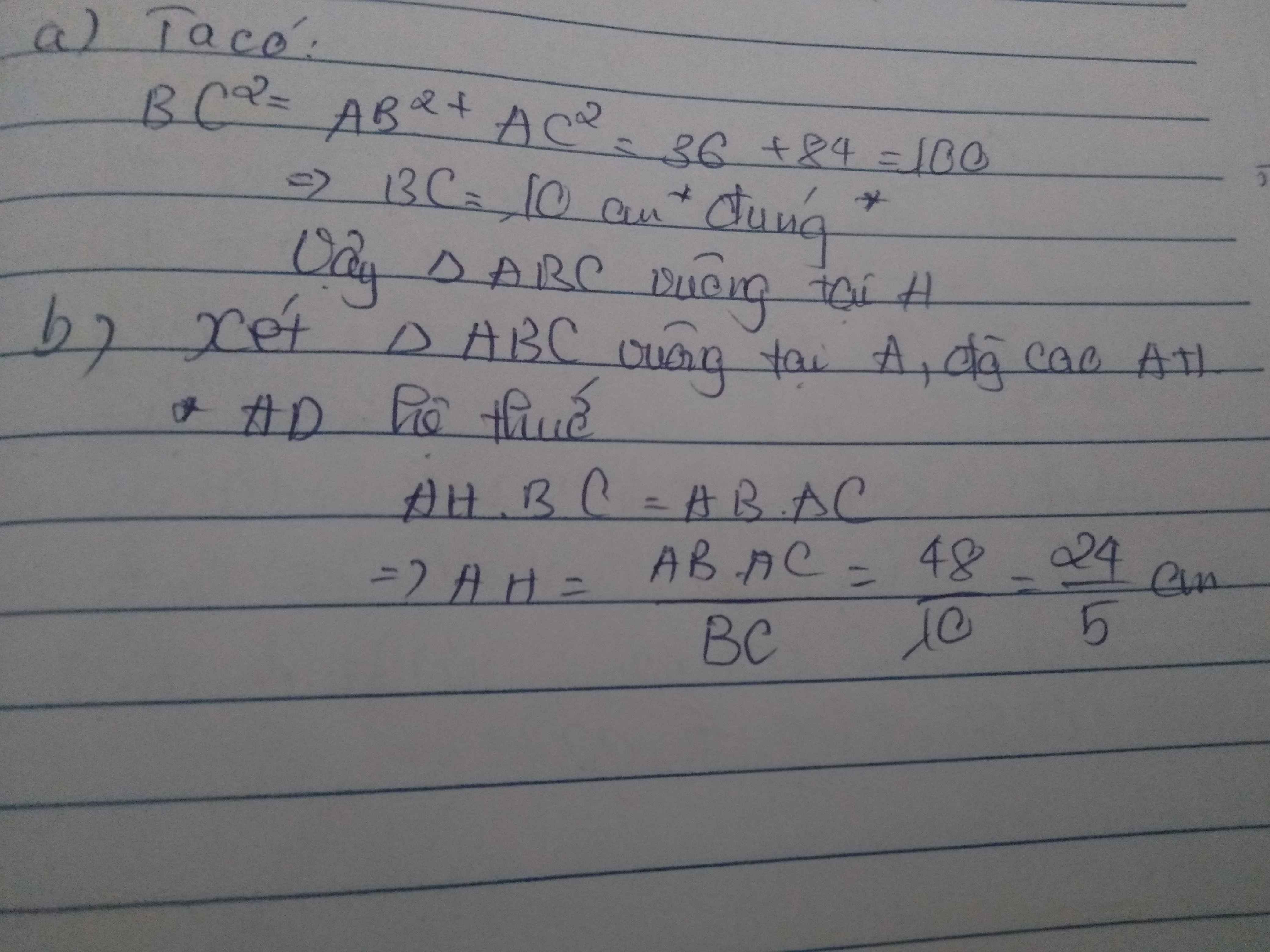Bài 19: Cho tam giác ABC có AC > AB. M là một điểm bất kỳ trên cạnh BC. Tìm vị trí
điểm M sao cho AM có độ dài nhỏ nhất.
Bài 20: Cho AB và CD là hai đoạn thẳng song song và bằng nhau. MN và PQ là các hình
chiếu của chúng trên cùng một đường thẳng khác. Chứng minh MN PQ.
Bài 21: Cho tam giác ABC vuông tại A, kẻ AH vuông góc BC ( H BC). Chứng minh:
AH + BC > AB + AC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 12 2021
bài 2:
ta có: AB<AC<BC(Vì 3cm<4cm<5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
LN
Lưu Nguyễn Hà An
CTVHS
15 tháng 2 2022
bài 2:
ta có: AB <AC <BC (Vì 3cm <4cm <5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
HT mik làm giống bạn Dương Mạnh Quyết
22 tháng 7 2021
1.
a. Ta có: \(AB^2+AC^2=6^2+8^2=36+64=100\)
\(BC^2=10^2=100\)
\(\Rightarrow AB^2+AC^2=BC^2\) \(\Rightarrow\Delta\)ABC vuông tại A
b. \(\Delta\)ABC vuông tại A, đường cao AH. Ta có:
AB.AC = AH.BC
hay 6.8 = AH.10
=> AH = \(\dfrac{6.8}{10}=4.8\)
