Câu 15 làm thế nào ạ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 1 2022
c: \(\widehat{FDH}=\widehat{ABE}\)
\(\widehat{EDH}=\widehat{ACF}\)
mà \(\widehat{ABE}=\widehat{ACF}\)
nên DH là tia phân giác của góc EDF
\(\widehat{FEH}=\widehat{BAD}\)
\(\widehat{DEH}=\widehat{FCB}\)
mà \(\widehat{BAD}=\widehat{FCB}\)
nên EH là tia phân giác của góc DEF
24 tháng 10 2021
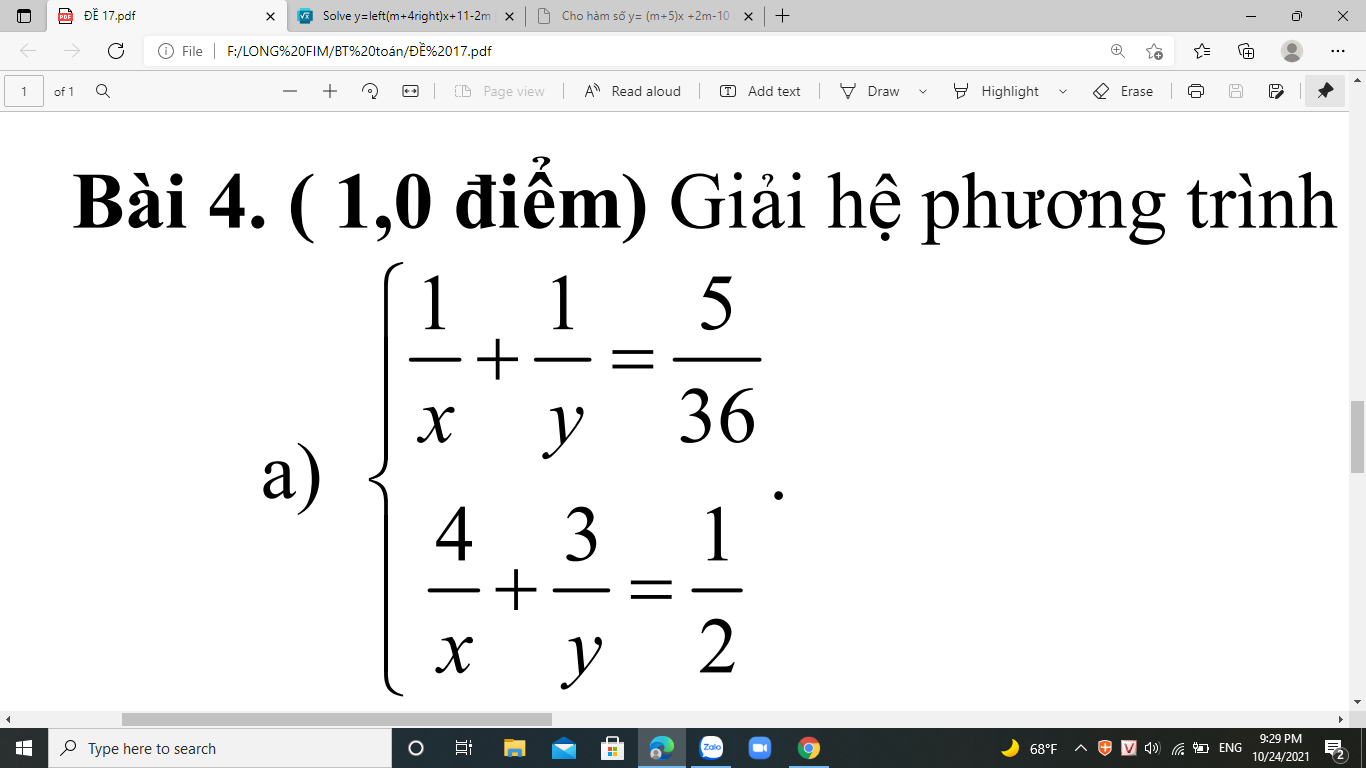
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{5}{36}\\\dfrac{4}{x}+\dfrac{3}{y}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{4}{y}=\dfrac{5}{9}\\\dfrac{4}{x}+\dfrac{3}{y}=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{y}=\dfrac{1}{18}\\\dfrac{1}{x}=\dfrac{1}{36}-\dfrac{1}{18}=-\dfrac{1}{36}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=18\\x=-36\end{matrix}\right.\)
2 tháng 6 2023
3: Gọi I là điểm đối xứng của O qua BC, OI cắt BC tại N
=>N là trung điểm chung của OI và BC và I,N cố định
BH//CD; CH//BD
=>BHCD là hbh
=>N là trung điểm của HD
ON là đường trung bình của ΔAHD
=>AH=2ON
=>AH=OI=2ON
AH//OI
=>AHOI là hbh
=>IH=OA=R
=>H thuộc (I;R) cố định
TP
17 tháng 11 2021
\(NaCl+AgNO_3\rightarrow NaNO_3+AgCl\\ n_{AgCl}=n_{NaCl}=0,5.2=1\left(mol\right)\\ \Rightarrow m_{AgCl}=1.143,5=143,5\left(g\right)\\ \Rightarrow ChọnA\)
H
25 tháng 5 2023
c. Dễ chứng minh 5 điểm A, N, F, H, E cùng thuộc đường tròn đường kính AH.
\(\Rightarrow HN\perp AN\left(1\right)\)
Vẽ đường kính AM của (O) \(\Rightarrow MN\perp AN\left(2\right)\)
Từ (1), (2) suy ra 3 điểm M, H, N thẳng hàng (3)
Dễ chứng minh BHCM là hình bình hành (BH // CM do cùng vuông góc với AC, tương tự 2 cạnh còn lại)
\(\Rightarrow\) 3 điểm H, I, M thẳng hàng (4)
Từ (3), (4) suy ra 3 điểm N, H, I thẳng hàng.
HT
0
BV
2
10 tháng 8 2023
48 - 2 : x = 16
2 : x = 48 - 16 = 32
x = 2 : 32 = \(\dfrac{2}{32}=\dfrac{1}{16}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
11 tháng 2 2023
\(\dfrac{20\times30}{3\times6\times25}\) = \(\dfrac{4\times5\times6\times5}{3\times6\times5\times5}\) = \(\dfrac{5\times6\times5\times4}{5\times6\times5\times3}\) =\(\dfrac{4}{3}\)
\(\dfrac{15\times28}{35\times20}\) = \(\dfrac{5\times3\times7\times4}{5\times7\times4\times5}\) = \(\dfrac{5\times7\times4\times3}{5\times7\times4\times5}\) = \(\dfrac{3}{5}\)
Hàm trùng phương có 3 cực trị khi: \(ab< 0\)
Hay \(\left(m^2-4\right)\left(m^2-25\right)< 0\)
\(\Rightarrow4< m^2< 25\)
\(\Rightarrow\left[{}\begin{matrix}-5< m< -2\\2< m< 5\end{matrix}\right.\) \(\Rightarrow m=\left\{-4;-3;3;4\right\}\)