Cho \(a,b,c\ge1:\) \(\Sigma a+2 =\Pi a\) CMR
\(\Sigma bc\sqrt{a^2-1} \leq \frac{3\sqrt{3}}{2}.\Pi a\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 4 2020
Cm \(3\left(a^2b+b^2c+c^2a\right)\left(a^2c+b^2a+c^2b\right)\ge abc\left(a+b+c\right)^3\)
Do 2 vế BĐT đồng bậc nên ta chuẩn hóa \(a+b+c=3\)
BĐT <=> \(3\left[abc\left(a^3+b^3+c^3\right)+\left(a^3b^3+b^3c^3+a^3c^3\right)+a^2b^2c^2\left(a+b+c\right)\right]\ge27abc\)
<=>\(3\left[abc\left(a^3+b^3+c^3\right)+\left(a^3b^3+b^3c^3+a^3c^3+3a^2b^2c^2\right)\right]\ge27abc\)
Áp dụng BĐT Schur ta có:
\(a^3b^3+b^3c^3+a^3c^3+3a^2b^2c^2\ge ab^2c\left(ab+bc\right)+a^2bc\left(ab+ac\right)+abc^2\left(ac+bc\right)\)
Khi đó BĐT
<=>\(3\left(a^3+b^3+c^3\right)+3a^2\left(b+c\right)+3b^2\left(a+c\right)+3c^2\left(a+b\right)\ge27\)
<=> \(3\left(a^3+b^3+c^3\right)+3a^2\left(3-a\right)+3b^2\left(3-b\right)+3c^2\left(3-c\right)\ge27\)
<=> \(a^2+b^2+c^2\ge3\) luôn đúng do \(a^2+b^2+c^2\ge\frac{1}{3}\left(a+b+c\right)^2=3\)( ĐPCM)
Dấu bằng xảy ra khi a=b=c
26 tháng 5 2020
Bài 2
Áp dụng \(x^2+y^2\ge\frac{\left(x+y\right)^2}{2}\)
=> \(VT\ge\frac{|a+1-b|+|b+1-c|+|c+1-a|}{\sqrt{2}}\)
Áp dụng BĐT \(|x|+|y|+|z|\ge|x+y+z|\)
=> \(VT\ge\frac{|a+1-b+b+1-c+c+1-a|}{\sqrt{2}}=\frac{3}{\sqrt{2}}\)(ĐPCM)
Dấu bằng xảy ra khi \(a=b=c=\frac{1}{2}\)
UI
7
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 8 2021
\(\left(b^3+c^3\right)\left(1+1\right)\left(1+1\right)\ge\left(b+c\right)^3\)
\(\Rightarrow b^3+c^3\ge\dfrac{\left(b+c\right)^3}{4}\Rightarrow\dfrac{a}{\sqrt[3]{b^3+c^3}}\le\dfrac{a\sqrt[3]{4}}{b+c}\)
Tương tự và cộng lại:
\(VT\le\sqrt[3]{4}\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)< \sqrt[3]{4}\left(\dfrac{2a}{a+b+c}+\dfrac{2b}{a+b+c}+\dfrac{2c}{a+b+c}\right)=2\sqrt[3]{4}\)
13 tháng 4 2023
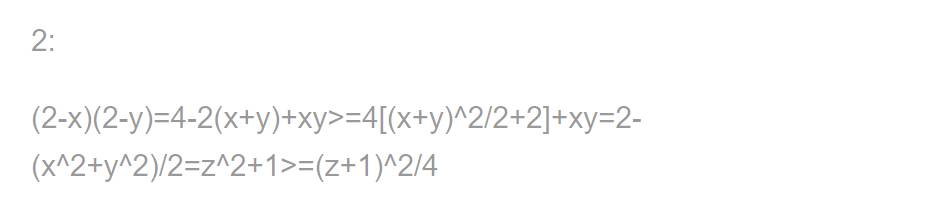
Tương tự, ta được:
\(\left(2-y\right)\left(2-z\right)>=\dfrac{\left(x+1\right)^2}{4}\)
và \(\left(2-z\right)\left(2-x\right)>=\left(\dfrac{y+1}{2}\right)^2\)
=>8(2-x)(2-y)(2-z)>=(x+1)(y+1)(z+1)
(x+yz)(y+zx)<=(x+y+yz+xz)^2/4=(x+y)^2*(z+1)^2/4<=(x^2+y^2)(z+1)^2/4
Tương tự, ta cũng co:
\(\left(y+xz\right)\left(z+y\right)< =\dfrac{\left(y^2+z^2\right)\left(x+1\right)^2}{2}\)
và \(\left(z+xy\right)\left(x+yz\right)< =\dfrac{\left(z^2+x^2\right)\left(y+1\right)^2}{2}\)
Do đó, ta được:
\(\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)< =\left(x+1\right)\left(y+1\right)\left(z+1\right)\)
=>ĐPCM
HQ
Hà Quang Minh
Giáo viên
5 tháng 11 2023
(a) Sai, liên kết đôi được tạo nên từ 1 liên kết $\sigma $ và 1 liên kết $\pi $.
(b) Sai, liên kết ba được tạo nên từ 1 liên kết $\sigma $và 2 liên kết $\pi $.
(c) Đúng.
(d) Sai.
N
1
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 2 2020
Sử dụng bổ đề: \(a^2+b^2+c^2+2abc+1\ge2\left(ab+bc+ca\right)\)
Cách chứng minh bổ đề kia bằng Dirichlet google rất nhiều.
Ta có: \(2a^2+2b^2+2c^2+2abc=8\)
\(\Leftrightarrow9=a^2+b^2+c^2+\left(a^2+b^2+c^2+2abc+1\right)\ge a^2+b^2+c^2+2\left(ab+bc+ca\right)\)
\(\Leftrightarrow9\ge\left(a+b+c\right)^2\Rightarrow a+b+c\le3\)
\(\Rightarrow3\left(a+b+c\right)\ge\left(a+b+c\right)^2\ge3\left(ab+bc+ca\right)\)
\(\Rightarrow a+b+c\ge ab+bc+ca=\frac{1}{2}\left[a\left(b+c\right)+b\left(c+a\right)+a\left(b+c\right)\right]\)
\(\Rightarrow a+b+c\ge\frac{1}{2}\left[a.2\sqrt{bc}+b.2\sqrt{ac}+c.2\sqrt{ab}\right]\)
Dấu "=" xảy ra khi \(a=b=c=1\)
Với dữ kiện đề bài \(a+b+c+2=abc\) ta đặt:
\(a=\frac{y+z}{x};b=\frac{x+z}{y};c=\frac{x+y}{z}\)
=> \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}\ge\frac{\left(x+y+z\right)^2}{2\left(xy+yz+xz\right)}\ge\frac{3\left(ab+bc+ac\right)}{2\left(ab+bc+ac\right)}=\frac{3}{2}\)
=> \(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\ge\frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2\ge\frac{3}{4}\)
BĐT<=> \(\sqrt{\frac{a^2-1}{a^2}}+\sqrt{\frac{b^2-1}{b^2}}+\sqrt{\frac{c^2-1}{c^2}}\le\frac{3\sqrt{3}}{2}\)
<=> \(\sqrt{1-\frac{1}{a^2}}+\sqrt{1-\frac{1}{b^2}}+\sqrt{1-\frac{1}{c^2}}\le\frac{3\sqrt{3}}{2}\)
Áp dụng BĐT buniacoxki cho VT ta có :
\(VT\le\sqrt{3.\left(3-\frac{1}{a^2}-\frac{1}{b^2}-\frac{1}{c^2}\right)}\le\sqrt{3\left(3-\frac{3}{4}\right)}=\frac{3\sqrt{3}}{2}\)(ĐPCM)
Dấu bằng xảy ra khi a=b=c=2
Khó quáaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa