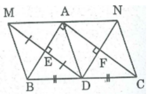
Cho tam giác ABC vuông tại A . Đường trung tuyến AN. Điểm M là hình chiếu vuông góc của N trên AB . Vẽ điểm Q đối xứng với điểm N qua AC . Gọi giao điểm của NQ và AC là P.
1) Các tứ giác AMNP,ANCQ là hình gì ?Vì sao ?
2) AN cắt MP tại điểm E. Chứng minh : ba điểm B,E,Q thẳng hàng.
3) Tam giác ABC có thêm điều kiện gì để tứ giác ABCQ là hình thang cân.
giúp mik với ạ , mình cảm ơn


1: Ta có: N và Q đối xứng nhau qua AC
nên AC là đường trung trực của NQ
Suy ra: P là trung điểm của NQ và AC\(\perp\)NQ tại P
Xét tứ giác AMNP có
\(\widehat{PAM}=\widehat{APN}=\widehat{AMN}=90^0\)
Do đó: AMNP là hình chữ nhật
Xét ΔABC có
N là trung điểm của BC
NP//AB
Do đó: P là trung điểm của AC
Xét tứ giác ANCQ có
P là trung điểm của AC
P là trung điểm của NP
Do đó: ANCQ là hình bình hành
mà AC\(\perp\)NQ
nên ANCQ là hình thoi