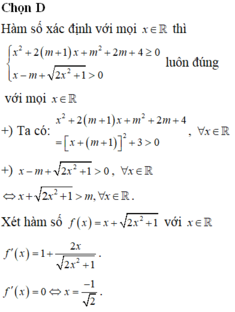có bao nhiêu giá trị nguyên của m để bpt sau có tập nghiệm là R?
x2 -2mx3 +3mx2 +4mx+4 ≥0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trường hợp 1: m=-1
Bất phương trình sẽ là \(0x^2-2\cdot0\cdot x+4>=0\)(luôn đúng)
Trường hợp 2: m<>-1
\(\text{Δ}=\left(2m+2\right)^2-4\cdot4\cdot\left(m+1\right)\)
\(=4m^2+8m+4-16m-16\)
\(=4m^2-8m-12\)
\(=4\left(m^2-2m-3\right)\)
Để bất phương trình có nghiệm đúng với mọi x thực thì \(\left\{{}\begin{matrix}\left(m-3\right)\left(m+1\right)< 0\\\left(m+1\right)>=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-1< m< 3\\m>=-1\end{matrix}\right.\Leftrightarrow-1< m< 3\)
Vậy: -1<=m<3

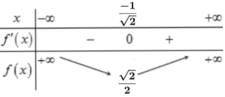
Điều kiện xác định x ∈ R
Đặt t = x 2 + 1 , t ≥ 1
Phương trình trở thành t 2 - 1 - 4 t - m + 1 = 0 ⇔ t 2 - 4 t = m 2
Để phương trình có 4 nghiệm phân biệt thì phương trình (2) có hai nghiệm phân biệt lớn hơn 1.
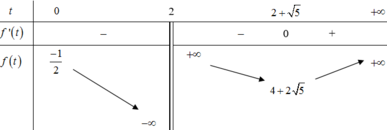
Xét hàm số f t = t 2 - 4 t có đồ thị là parabol có hoành độ đỉnh x = 2 ∈ 1 ; + ∞ nên ta có bảng biến thiên:
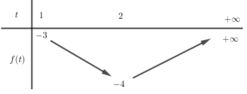
Dựa BBT ta thấy để (2) có hai nghiệm phân biệt lớn hơn 1 thì - 4 < m < - 3
Vậy không có giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Đáp án cần chọn là: B

TH1: m+1=0 <=> m=-1
Khi đó bpt là -2(-1+1)x+4 >= 0 <=> -4x+4 >= 0 <=> x<=1 (KTM S=R) => loại
TH2: m+1 khác 0 <=> m khác -1
Để bpt (m+1)x2 -2(m+1)x+4 ≥ 0 có nghiệm với mọi x
<=>
<=>
Vậy m>3 thì...