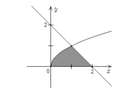
Cho hình phẳng (H) được giới hạn bởi đường cong (C) y=e^x,trục Õ, trục Oy và đường thẳng x=2. Diện tích của hp (H) là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Phương trình hoành độ giao điểm của đường cong y = tan x trục hoành là tan x = 0 ⇔ x = k π
V = π ∫ 0 π 4 tan 2 x d x = π ∫ 0 π 4 1 cos 2 x - 1 d x = π tanx - x 0 π 4 = π 1 - π 4

Thể tích vật thể tròn xoay cần tìm là
V = π ∫ 0 2 x 2 dy = π ∫ 0 2 y 4 dy = 32 π 5
Đáp án B

Đáp án B
Thể tích khối tròn xoay cần tính là V = π ∫ 1 e f 2 x d x = π ∫ 1 e ln 2 x x d x
Đặt t = ln x ⇔ d t = d x x và x = 1 ⇒ t = 0 x = e ⇒ t = 1 . Khi đó ∫ 1 e ln 2 x x d x = ∫ 0 1 t 2 d t = t 3 3 0 1 = 1 3 . Vậy V = π 3

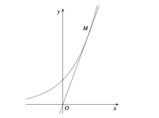
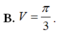
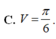

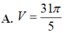
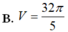
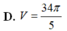
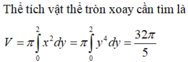

Do \(e^x>0;\forall x\)
Diện tích hình phẳng:
\(S=\int\limits^2_0e^xdx=e^x|^2_0=e^2-1\)