cho tam giác ABC, đường thẳng a cắt AB và AC lần lượt tại hai điểm D và E ( a song song BC ).Biết AD bằng √3, DB bằng 5 ; EC bằng 10. Tính độ dài đoạn thẳng AE ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do DE song song BC
=> Theo định lý Talet, DA/DB = EA/EC
Mà DA/DB= EC/EA
=> EC=EA
=> E là trung điểm AC
=> DE là đường trung bình của tam giác ABC
=> D cũng là trung điểm AB

gggggjjjk..hhhyh iuugln............................lklhuluiiiihhhhhhh ok-

b1 :
DE // AB
=> góc ABC = góc DEC (đồng vị)
góc ABC = góc ACB do tam giác ABC cân tại A (gt)
=> góc DEC = góc ACB
=> tam giác DEC cân tại D (dh)
b2:
a, tam giác ABC => góc A + góc B + góc C = 180 (đl)
góc A = 80; góc B = 50
=> góc C = 50
=> góc B = góc C
=> tam giác ABC cân tại A (dh)
b, DE // BC
=> góc EDA = góc ABC (slt)
góc DEA = góc ECB (dlt)
góc ABC = góc ACB (Câu a)
=> góc EDA = góc DEA
=> tam giác DEA cân tại A (dh)
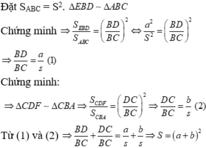
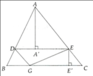
Theo định lý Thales trong tam giác ABC, ta có: \(\frac{AD}{DB}=\frac{AE}{EC}\Leftrightarrow\frac{\sqrt{3}}{5}=\frac{AE}{10}\Leftrightarrow AE=\frac{10\sqrt{3}}{5}\)
KL: Vậy ..............