HELP!!! Mn giúp mk câu này với!!! 😓😓
Tìm x biết:
(2x + 1) tất cả mũ 2 - 4/9 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 7 2021
4) Ta có: ADB = BDC
Mà 2 góc này ở vị trí so le trong
=> AB//CD
Đúng thì like giúp mik nhé. Thx bạn
16 tháng 7 2021
3) Dy//Ct vì \(\widehat{tCd}+\widehat{yDC}=180^0\) và \(\widehat{tCd}\); \(\widehat{yDC}\) là hai góc trong cùng phía
16 tháng 7 2021
1, a và b có song song vì \(\)có 2 góc =70 độ ở vị trí so le trong
2.Mx và Ny có song song do góc M =góc N và 2 góc ở vị trí đônhg vị
3.Ct và Dy có song song vì góc C+ góc D=180 độ và 2 góc này ở vị trí trong cùng phía
4. có AD song song BC vì góc ADB=góc DBC
và 2 góc ở vị trí so le trong
TG
16 tháng 7 2021
4:
Có: Góc ADB = Góc DBC (GT)
Mà 2 góc này là 2 góc so le trong
=> AD // BC
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 12 2022
42.
ĐKXĐ: \(x>0\)
\(log_3^2x-5log_3x+6\le0\)
\(\Leftrightarrow\left(log_3x-2\right)\left(log_3x-3\right)\le0\)
\(\Rightarrow2\le log_3x\le3\)
\(\Rightarrow9\le x\le27\)
\(\Rightarrow2a-b=9.2-27=\)
43.
\(r=\dfrac{1}{2};h=1\)
\(\Rightarrow V=\pi r^2h=\dfrac{\pi}{4}\)
44.
ĐKXĐ: \(a>0\)
\(log_2a+log_23=log_2\left(2a+2\right)\)
\(\Leftrightarrow log_2\left(3a\right)=log_2\left(2a+2\right)\)
\(\Rightarrow3a=2a+2\)
\(\Rightarrow a=2\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 12 2022
45.
\(V=\dfrac{1}{3}.6a.20a^2=40a^3\)
46.
Pt hoành độ giao điểm:
\(-x^2+2=x^3+2\Leftrightarrow x^3+x^2=0\)
\(\Leftrightarrow x^2\left(x+1\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)
\(\Rightarrow\) Hai đồ thị có 2 giao điểm
47.
\(y'=x^2-5x+6=0\Rightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
\(f\left(1\right)=\dfrac{29}{6}\) ; \(f\left(2\right)=\dfrac{17}{3}\) ; \(f\left(3\right)=\dfrac{11}{2}\)
\(\Rightarrow\) Hàm đạt min tại \(x=1\) và đạt max tại \(x=2\)
\(\Rightarrow x_1+x_2=3\)
48.
\(y'=-4x^3=0\Rightarrow x=0\)
Do \(a=-1< 0\Rightarrow\)hàm đồng biến trên \(\left(-\infty;0\right)\)
49.
\(y'=3ax^2+2bx+c\Rightarrow\left\{{}\begin{matrix}c=0\\12a+4b+c=0\end{matrix}\right.\)
\(x=0;y=d\Rightarrow d=2\)
\(x=2;y=-2\Rightarrow8a+4b+2c+d=-2\)
\(\Rightarrow8a+4b+2=-2\Rightarrow\left\{{}\begin{matrix}12a+4b=0\\8a+4b=-4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-3\end{matrix}\right.\)
\(\Rightarrow y=x^3-3x^2+2\)
\(\Rightarrow y\left(-2\right)=-18\)
DD
Đoàn Đức Hà
Giáo viên
26 tháng 12 2022
Câu 3:
Phương trình hoành độ giao điểm: \(-x=x^3\Leftrightarrow x^3+x=0\Leftrightarrow x\left(x^2+1\right)=0\Leftrightarrow x=0\).
Phương trình có \(1\) nghiệm do đó chọn C.
DD
Đoàn Đức Hà
Giáo viên
26 tháng 12 2022
Câu 4:
\(2^{2x^2-7x+5}=32\)
\(\Leftrightarrow2^{2x^2-7x+5}=2^5\)
\(\Leftrightarrow2x^2-7x+5=5\)
\(\Leftrightarrow2x^2-7x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{7}{2}\end{matrix}\right.\)
Suy ra \(x_1=0,x_2=\dfrac{7}{2}\).
\(x_1+4x_2=14\).
Chọn A.
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2022
24.
\(log\left(a^3b^2\right)=loga^3+logb^2=3loga+2logb=3x+2y\)
25.
\(f'\left(x\right)=0\) có 2 nghiệm bội lẻ \(x=\left\{-\dfrac{3}{2};1\right\}\) nên hàm có 2 cực trị
26.
\(\lim\limits_{x\rightarrow\infty}\dfrac{x^2+3x-4}{x^2-16}=\lim\limits_{x\rightarrow\pm\infty}\dfrac{1+\dfrac{3}{x}-\dfrac{4}{x^2}}{1-\dfrac{16}{x^2}}=1\)
\(\Rightarrow y=1\) là TCN của đồ thị hàm số
\(\lim\limits_{x\rightarrow-4}\dfrac{x^2+3x-4}{x^2-16}=\lim\limits_{x\rightarrow-4}\dfrac{\left(x-1\right)\left(x+4\right)}{\left(x-4\right)\left(x+4\right)}=\lim\limits_{x\rightarrow-4}\dfrac{x-1}{x-4}=\dfrac{5}{8}\) hữu hạn
\(\Rightarrow x=-4\) không phải tiệm cận đứng
\(\lim\limits_{x\rightarrow4^+}\dfrac{x^2+3x-4}{x^2-16}=+\infty\Rightarrow x=4\) là 1 TCĐ
Vậy đồ thị hàm số có 2 tiệm cận
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2022
27.
\(y'=x^2-2x+2\)
\(y'\left(1\right)=1\)
\(y\left(1\right)=\dfrac{7}{3}\)
Phương trình tiếp tuyến có dạng:
\(y=1\left(x-1\right)+\dfrac{7}{3}\Leftrightarrow y=x+\dfrac{4}{3}\)
28.
ĐKXĐ: \(x>0\)
\(\log x\le1\)
\(\Rightarrow x\le10\)
Kết hợp ĐKXĐ ta được \(x\in(0;10]\)
29.
Gọi H là trung điểm AB \(\Rightarrow SH\perp\left(ABCD\right)\)
Do SAB vuông cân tại S \(\Rightarrow SH=\dfrac{1}{2}AB=\dfrac{a}{2}\)
\(\Rightarrow V=\dfrac{1}{3}SH.a^2=\dfrac{a^3}{6}\)
17 tháng 1 2022
Câu 16.
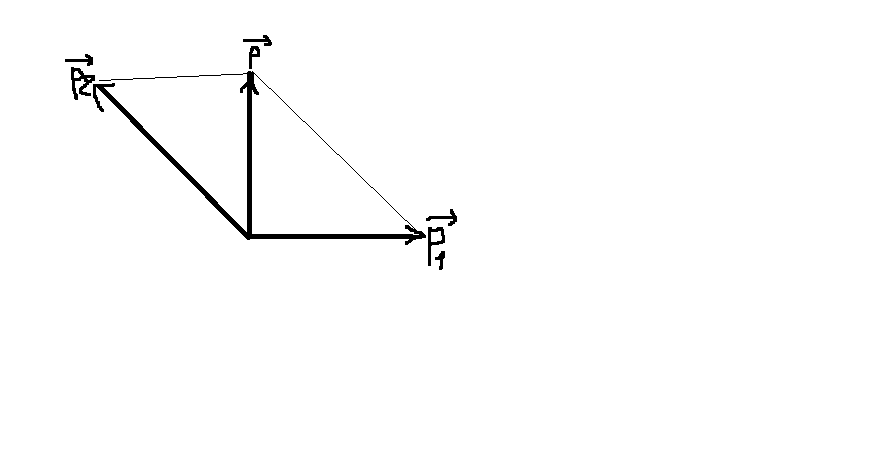
Hình vẽ tương đối thôi nha!!!
Bảo toàn động lương ta có:
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
\(\Rightarrow p^2=p_2^2-p_1^2\)\(\Rightarrow p_2=\sqrt{p^2+p_1^2}\)
\(\Rightarrow m_2\cdot v_2=\sqrt{\left(m_1+m_2\right)\cdot v+m_1\cdot v_1}\)
\(\Rightarrow0,3\cdot v_2=\sqrt{[\left(0,5+0,3\right)\cdot3]^2+(0,5\cdot4)^2}=3,124\)
\(\Rightarrow v_2=10,41\)m/s
NG
15 tháng 10 2020
\(\frac{x}{-9}=\frac{y}{12}\text{ và }2.x-3.y=163\left(1\right)\)
\(\text{C1: Ta có: }\frac{x}{-9}=\frac{y}{12}=k\)
\(\Leftrightarrow x=-9.k\text{ }\text{ }\text{ }\text{ }\)
\(\Leftrightarrow y=12.k\)
\(\text{Thay x=-9k, y=12k vào (1), ta được: }\)
\(2.\left(-9\right).k-3.12.k=163\)
\(\Leftrightarrow-18.k-36.k=163\)
\(\Leftrightarrow k.\left(-18-36\right)=163\)
\(\Leftrightarrow k.\left(-54\right)=163\)
\(\Leftrightarrow k=\frac{163}{-54}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\frac{163}{-54}.\left(-9\right)\\y=\frac{163}{-54}.12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\frac{163}{6}\\y=\frac{326}{-9}\end{matrix}\right.\)
\(\text{Vậy }\left(x,y\right)=\frac{163}{6},\frac{326}{-9}\)
\(\text{C2: Ta có: }\frac{x}{-9}=\frac{y}{12}\Rightarrow\frac{2x}{-18}=\frac{3y}{36}\)
\(\Rightarrow\frac{2x}{-18}=\frac{3y}{36}=\frac{2x-3y}{-18-36}\left(2\right)\)
\(\text{Thay (1) vào (2), ta được: }\)
\(\Rightarrow\frac{2x}{-18}=\frac{3y}{36}=\frac{2x-3y}{-18-36}=\frac{163}{-54}\)
\(\left(\text{Chỗ này bạn có thể thay luôn vào dòng trên không cần phải ghi cái dòng trên là thay đâu}\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}\frac{x}{-9}=\frac{163}{-54}\\\frac{y}{12}=\frac{163}{-54}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\frac{163}{-54}.\left(-9\right)\\y=\frac{163}{-54}.12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\frac{163}{6}\\y=\frac{326}{-9}\end{matrix}\right.\)
\(\text{Vậy }\left(x,y\right)=\frac{163}{6},\frac{326}{-9}\)
\(\left(2x+1\right)^2-\frac{4}{9}=0\)
\(\Leftrightarrow\left(2x+1\right)^2=\frac{4}{9}\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(2x+1\right)^2=\left(\frac{2}{3}\right)^2\\\left(2x+1\right)^2=\left(-\frac{2}{3}\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=\frac{2}{3}\\2x+1=-\frac{2}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=-\frac{1}{3}\\2x=-\frac{5}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\frac{1}{6}\\x=-\frac{5}{6}\end{matrix}\right.\)
Vậy \(x\in\left\{-\frac{1}{6};-\frac{5}{6}\right\}\)
WTF?? Ai cho làm như thế?? Vậy mà cũng được tick?? Có nhầm không vậy?? Các bác nói một câu công bằng xem nào!!! Có vụ bỏ cả BP ở 2 vế được luôn cơ à?? Bức xúc thật đấy!!