Cho hbh ABCD. Gọi O là tâm đường tròn nội tiếp tam giác ABC
Biết khoảng cách từ O đến A và 2 đường thẳng AD và AC tương ứng là 5,4,3
tính diện tích hình bình hành ABCD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

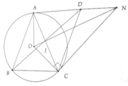
a, Tam giác ABC cân tại A nội tiếp (O)
=> OA ⊥ BC
=> OA ⊥ AD (vì AD//BC)
=> AD là tiếp tuyến của (O)
b, Chứng minh được ON là tia phân giác của A O D ^ mà ∆OAC cân tại O nên ON cũng là đường trung tuyến => ON cắt AC tại trung điểm I của AC => ON,AC,BD cùng đi qua trung điểm I của AC

Đáp án: D.
Hướng dẫn giải:
Lấy M là trung điểm BC, H là hình chiếu của A lên SM. Xác định
![]()
S A ⊥ B C ⊥ A M
![]()
⇒ A H ⊥ S M ⇒ A H ⊥ ( S B C )
⇒ d ( A , ( S B C ) ) = A H
Vì AD//(SBC) chứa BC nên
d(SB,AD)=d(AD,(ABC))=d(A,(SBC))=AH
Tính: SA=AD= a 2 ,AM= a 2
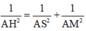
⇒ A H = a 2 5

Lời giải:
a)
$\widehat{ABD}=\widehat{DCA}=90^0$ (góc nt chắn nửa đường tròn)
$\Leftrightarrow \widehat{ABE}=\widehat{DCE}=90^0$
Tứ giác $ABEH$ có tổng 2 góc đối $\widehat{ABE}+\widehat{AHE}=90^0+90^0=180^0$ nên là tứ giác nội tiếp.
Tứ giác $DCEH$ có tổng 2 góc đối $\widehat{DCE}+\widehat{EHD}=90^0+90^0=180^0$ nên là tứ giác nội tiếp.
b)
Từ 2 tứ giác nội tiếp phần a, kết hợp với $ABCD$ là tứ giác nội tiếp, ta có:
\(\widehat{HBE}=\widehat{EAH}=\widehat{CAD}=\widehat{CBD}=\widehat{CBE}\) nên $BE$ là tia phân giác $\widehat{HBC}$
\(\widehat{HCE}=\widehat{EDH}=\widehat{BDA}=\widehat{BCA}=\widehat{BCE}\) nên $CE$ là tia phân giác $\widehat{BCH}$
Do đó $E$ chính là tâm đường tròn nội tiếp tam giác $BCH$
c) Sử dụng tính chất trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền. Suy ra $IH=IC=EI=ID$.
Ta có:
\(\widehat{IHD}=\widehat{IDH}=\widehat{ODB}=\widehat{OBD}=\widehat{OBI}\) nên $OBIH$ là tứ giác nội tiếp $(1)$
Mặt khác:
$\widehat{HIC}=\widehat{HIB}+\widehat{CIB}$
$=2\widehat{IDH}+2\widehat{CDI}$
$=2\widehat{HDC}=2\widehat{ADC}=2(90^0-\widehat{CAD})$
$=180^0-2\widehat{CBE}=180^0-\widehat{CBH}$
$\Rightarrow BHIC$ là tứ giác nội tiếp $(2)$
Từ $(1);(2)$ suy ra đpcm.

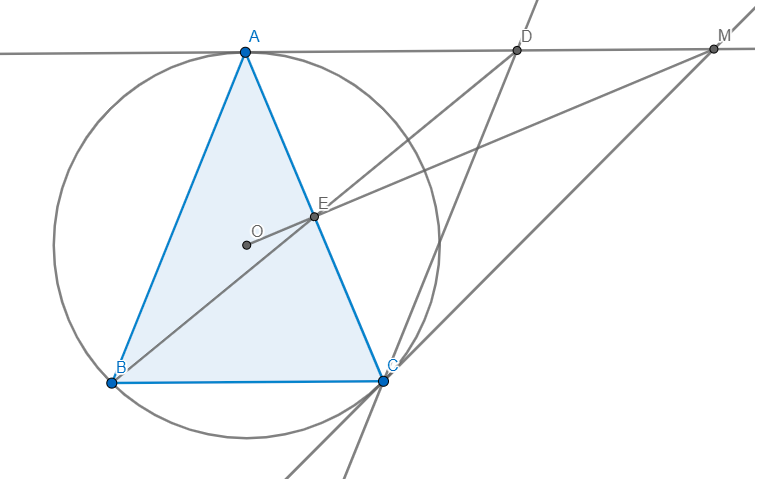
a) Vì tam giác ABC cân tại A \(\Rightarrow AB=AC\)
Vì O là tâm (ABC) \(\Rightarrow OB=OC\Rightarrow OA\) là trung trực BC
\(\Rightarrow OA\bot BC\) mà \(BC\parallel AD\Rightarrow AD\bot OA\) \(\Rightarrow AD\) là tiếp tuyến
b) MO cắt AC tại E.
Vì MC,MA là tiếp tuyến \(\Rightarrow\Delta MAC\) cân tại M và MO là phân giác \(\angle AMC\)
\(\Rightarrow E\) là trung điểm AC
Vì ABCD là hình bình hành có E là trung điểm AC \(\Rightarrow B,E,D\) thẳng hàng
\(\Rightarrow AC,BD,OM\) đồng quy tại E

a ) OA \(\perp\)BC
BC // AD
=> OA \(\perp\)AD => AD là tiếp tuyến tại A của đường tròn
b) ON cắt AC tại trung điểm của AC ( ON \(\perp\)AC sử dụng đường kính và dây đường tròn )
Lại có : ABCD là hình bình hành
=> BD cắt AC tại trung điểm của AC
=> Ba đường thẳng AC, BD,ON đồng quy
Chỉ là cách làm thôi bạn tự bổ sung nhé !
Bài này bạn chia làm 2 trường hợp Q thuộc đoạn AD và Q nằm ngoài AD
Từ gt => OA=5, OQ=4, và OM=ON=OP=3
Áp dụng định lý Pytago cho các tam giác QAO và tam giác MAO vuông ứng ứng lần lượt tại Q và M ta có:
AQ2=AO2-OQ2=52-42=32 => AQ+3
AM2=AO2-OM2=52-32=42 => AM=4
=> AM=QO và AQ=MO => AMOQ là hình bình hành
Mà \(\widehat{AMO}=90^o\) => AMOQ là hình chữ nhật
=> \(\widehat{QAM}=90^o\)
Từ đó ta có ABCD là hình chữ nhật
Đặt CP=CN=x
Áp dụng định lý Pytago cho tam giác ABC vuông tại B, với BM=ON=3
AP=AM=4; AB=AM+BM=7
ta có: CA2=AB2+BC2 <=> (x+4)2=72+(x+3)2
=> x=21 và BC=24
Vậy diện tích hình bình hành ABCD là 7.24=168 (đv diện tích)
Cmtt trường hợp 1 ta tính được
\(\widehat{ACB}=90^o;AC=7;BC=24\)
Từ đó ta tính được
SABCD=168 (đv diện tích)