Cho ΔABCnhọn, đường cao BD, CE cắt nhau tại H
a) Chứng minh rằng AD.AC = AE.AB và ^ABC= ^ADE
b) Chứng minh rằng ΔHEDvà ΔHBCđồng dạng
c)Chứng minh rằng BE.BA CD.CA = BC²
d) Nếu ΔABCđều hãy tính tỉ số diện tíchΔHEDvà diện tích ΔABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
I
9 tháng 4 2020
a) xét \(\Delta ADB\)zà \(\Delta AEC\)có
\(\hept{\begin{cases}\widehat{A}chung\\\widehat{AEC}=\widehat{ADB}=90^0\end{cases}}\)
\(=>\Delta ADB~\Delta AEC\left(g.g\right)\)
\(=>\frac{AD}{AE}=\frac{AB}{AC}=>AD.AC=AB.AE\left(dpcm\right)\)
\(taco\left(\frac{AD}{AE}=\frac{AB}{AC}=>\frac{AD}{AB}=\frac{AE}{AC}\right)\)
xét \(\Delta ADE\)zà \(\Delta ABCco\)
\(\hept{\begin{cases}\widehat{A}chung\\\frac{AD}{AB}=\frac{AE}{AC}\end{cases}=>\Delta ABE~\Delta ABC\left(c.g.c\right)}\)
=>\(\widehat{ADE}=\widehat{ABC}\left(dpcm\right)\)
I
9 tháng 4 2020
c) Xét tam giác AEC zà tam giác HDC óc
góc AEC= góc HDC =90 độ
góc HCE chung
=> tam giác AEC~ tam giác HDC
=>\(\frac{AC}{HC}=\frac{EC}{DC}=>AC.DC=EC.HC\left(1\right)\)
xét tam giác BEC zà tam giác HEA có
góc BEC= góc AEH= 90 độ
góc BCE = góc EAH ( cùng phụ zới góc EBC )
=> tam giác BEC ~ tam giác HEA (g.g)
=>\(\frac{BE}{HE}=\frac{EC}{EA}=>BE.EA=EC.HE\left(2\right)\)
từ 1 zà 2 suy ra
\(BE.BA+CD.CA=BH.BD+CH.CE\)
kẻ AH zuông goc zới BC cắt BC tại F
Tự CM \(\hept{\begin{cases}\Delta CFH~\Delta CEB\\\Delta BFH~\Delta BDC\end{cases}=>\hept{\begin{cases}CF.CB=CH.CE\\BF.BC=BH.BD\end{cases}=>BE.BA+CD.CA=CF.CB+BF.CB}}\)
\(=BC.\left(CF+BF\right)=BC^2\)
22 tháng 4 2023
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạngvới ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AE*AB và AD/AB=AE/AC
b: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
=>ΔADE đồng dạng vói ΔABC
=>góc ADE=góc ABC
d: ΔADE đồng dạng với ΔABC
=>\(\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{AD}{AB}\right)^2=\dfrac{1}{4}\)
=>\(S_{ADE}=30\left(cm^2\right)\)
CM
4 tháng 10 2017
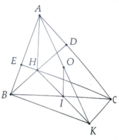
a, BHCK có I là trung điểm hai đường chéo
b, Ta có ∆ABK, ∆ACK vuông tại B và C nên A,B,K,C nằm trên đường tròn đường kính AK
c, Ta có OI là đường trung bình của ∆AHK => OI//AH
d, Gọi AH cắt BC tại M. Ta có BE.BA = BM.BC và CA.CD = CM.BC => ĐPCM
Cảm ơn