Cho tam giác ABC vuông tại A có góc B bằng 450 và cạnh AB bằng 3cm. Hãy tính BC
Giúp mình với ạh! Mình cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 7 2023
\(AH^2=BH.CH=18.32=576\Rightarrow AH=24\left(cm\right)\)
\(AB^2=AH^2+BH^2=576+324=900\) (Δ ABH vuông tại H)
\(\Rightarrow AB=30\left(cm\right)\)
\(AC^2=AH^2+CH^2=576+1024=1600\) (Δ ACH vuông tại H)
\(\Rightarrow AC=40\left(cm\right)\)
31 tháng 7 2023
Xét tam giác AHB vuông tại H có:
AH2+HB2=AB2(định lý pythagore) (1)
Xét tam giác AHC vuông tại H có:
HA2+HC2=AC2 (định lý pythagore) (2)
Từ (1) và (2) ta cộng lại vế theo vế, có:
2AH2+BH2+CH2=AB2+AC2
<=>2AH2+BH2+CH2=BC2
<=> 2AH2+182+322=(18+32)2
<=>2AH2+1348=2500
<=>2AH2=2500-1348
<=>2AH2=1152
<=>AH2=1152:2
<=>AH2=576
<=>AH=\(\sqrt{576}\)
<=>AH=24(cm)
-Ta thay AH=24cm vào (1) ta có:
HB2+AH2=AB2
<=>182+242=AB2
<=>900=AB2
<=>\(AB=\sqrt{900}=30\)(cm)
-Ta thay AH=24cm vào (2) ta có:
HC2+HA2=AC2
<=>322+242=AC2
<=>1600=AC2
\(\Leftrightarrow AC=\sqrt{1600}=40\left(cm\right)\)
Vậy AB=30cm; AC=40cm
20 tháng 10 2023
a: Đặt \(\dfrac{AB}{5}=\dfrac{AC}{12}=k\)
=>AB=5k; AC=12k
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(25k^2+144k^2=26^2\)
=>\(k^2=4\)
=>k=2
=>AB=10cm; AC=24cm
b: Xét tứ giác ABCD có
\(\widehat{A}+\widehat{B}+\widehat{BCD}+\widehat{ADC}=360^0\)
=>\(\widehat{BCD}+\widehat{ADC}=360^0-70^0=290^0\)
=>\(2\cdot\left(\widehat{ODC}+\widehat{OCD}\right)=290^0\)
=>\(\widehat{OCD}+\widehat{ODC}=145^0\)
Xét ΔOCD có \(\widehat{COD}+\widehat{OCD}+\widehat{ODC}=180^0\)
=>\(\widehat{COD}=180^0-145^0=35^0\)
PH
5 tháng 7 2017
vì tam giác abc vuông
=> BC^2 = AB^2 + AC^2 (Định lý pytago)
Thay AB=4cm; AC=3cm
Ta đc: BC^2= 4^2+3^2
BC^2=16+9
BC^2=25
=>BC=5cm
1 tháng 8 2023
Ta có :
\(AH^2=AB^2+BH^2\left(1\right)\) (Δ ABH vuông tại H)
\(AH^2=AC^2+CH^2\left(2\right)\) (Δ ACH vuông tại H)
\(\left(1\right),\left(2\right)\Rightarrow AB^2+BH^2=AC^2+CH^2\)
\(\Rightarrow CH^2=AB^2+BH^2-AC^2\)
\(\Rightarrow CH^2=81+676-121=636\)
\(\Rightarrow CH=\sqrt[]{636}=\sqrt[]{4.159}=2\sqrt[]{159}\left(cm\right)\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
31 tháng 7 2023
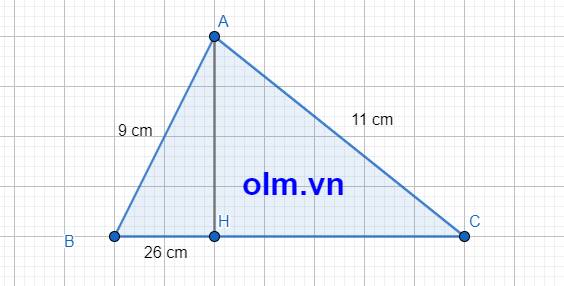
Vì AH là đường cao của tam giác ABC nên AH \(\perp\) BC \(\equiv\) H
⇒ \(\Delta\) AHB \(\perp\) \(\equiv\) H \(\Rightarrow\) AB > BH ⇒ 9 cm > 26 cm vô lý
Em có hai sựa lựa chọn: 1 là em chỉ ra cái sai của cô
2 là em xem lại đề bài của em
14 tháng 7 2023
Bài 3 :
\(BC=HC+HB=16+9=25\left(cm\right)\)
\(BC^2=AB^2+AC^2\Rightarrow AB^2=BC^2-AC^2=25^2-20^2=625-400=225=15^2\)
\(\Rightarrow AB=15\left(cm\right)\)
\(AH^2=HC.HB=16.9=4^2.3^2\Rightarrow AH=3.4=12\left(cm\right)\)
Bài 6:
\(AB=AC=4\left(cm\right)\) (Δ ABC cân tại A)
\(BH=HC=2\left(cm\right)\) (Ah là đường cao, đường trung tuyến cân Δ ABC)
\(BC=BH+HC=2+2=4\left(cm\right)\)
Chu vi Δ ABC :
\(4+4+4=12\left(cm\right)\)
\(\widehat{B}\)=\(45^0\) chứ
Ta có : B + C = 900 ( phụ nhau )
450 + C = 900
C = 900 - 450 = 450
=> Tam giác vuông ABC cũng là tam giác cân ABC cân tại A ( hai góc ở đáy bằng nhau )
=> AB = AC = 3cm
Áp dụng định lí Pytago vào tam giác vuông cân ABC ta có :
AB2 + AC2 = BC2
32 + 32 = BC2
9 + 9 = BC2
=> BC2 = 18
Ta có \(\sqrt{18}=3\sqrt{2}\)nên BC = \(3\sqrt{2}cm\)