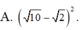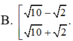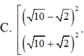có tồn tại các số tự nhiên x,y sao cho:
a)24x+2y=2020 b)30x-4y=2019
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
BD
1
DT
Dương Thị Yến Nhi A
8 tháng 4 2020
- a) có b) không
Đúng(0)
Những câu hỏi liên quan
QO
1
NT
0
Z
2
6 tháng 8 2015
b,30x + 4y = 1975
28x + 4y + 2x = 1975
=>4(7x + y)+2y = 1975
Ta thấy hai số hạng đều là số chẵn mà chẵn + chẵn = chẵn nên x,y không tồn tại
mình nhầm ấn nút gửi câu hỏi!
28 tháng 10 2018
(a) 24x + 3y = 2005
24x chia hết cho 3 3y chia hết cho 3
=> 24x + 3y chia hết cho 3
=> 2005 chia hết cho 3(vô lý)
Vậy ko tồn tại số tự ngiên x , y
TD
1
PL
1
CL
25 tháng 6 2015
24 chia hết 3 ; 3 chia hết 3 suy ra 24x + 3y chia hết 3
a ) Vì 2005 ko chia hết cho 3 nên ko tồn tại x , y
30 chia hết 2 ; 4 chia hết 2 suy ra 30x - 4y chia hết 2
b ) Vì 1975 ko chia hết cho 2 nên ko tồn tại x , y
CM
1 tháng 5 2019
Chọn C.
Phương pháp: Đưa bài toán về tìm m để hệ có nghiệm duy nhất.
CM
2 tháng 6 2017
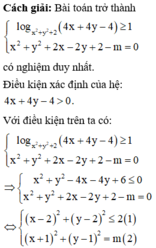
log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1
⇔ 4 x + 4 y - 4 ≥ x 2 + y 2 + 2 ⇔ x - 2 2 + y - 2 2 ≤ 2
Đây là tập hợp tất cả các điểm nằm trên và trong đường tròn tâm I(2;2) bán kính ℝ ' = m .
Ta có I I ' = 10 . m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 thì hai đường tròn nói trên tiếp xúc ngoài
⇒ R + R ' = I I ' ⇔ m + 2 = 10 ⇔ m = 10 - 2 2
Đáp án cần chọn là B