chứng minh rằng 2x-x2≤1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 7 2021
a) Ta có: \(\dfrac{x^2+2x+1}{x^2+x}\)
\(=\dfrac{\left(x+1\right)^2}{x\left(x+1\right)}\)
\(=\dfrac{x+1}{x}\)
b) Ta có: \(\dfrac{x^2-4x+3}{x^2-x}\)
\(=\dfrac{\left(x-1\right)\left(x-3\right)}{x\left(x-1\right)}\)
\(=\dfrac{x-3}{x}\)
CM
20 tháng 9 2019
Ta có:
+ Phương trình - 2x = 4 ⇔ x = - 2 có tập nghiệm là S = {- 2}
+ Phương trình x/2 = - 1 ⇔ x = - 2 có tập nghiệm là S = {- 2}
→ Hai phương trình có cùng tập nghiệm.
→ Hai phương trình tương đương.
OY
21 tháng 10 2021
a) \(2x^2+2x+1=0\)
\(\Rightarrow2x^2+2x=-1\)
\(\Rightarrow2x\left(x+1\right)=-1\)
⇒ Pt vô nghiệm
21 tháng 10 2021
a: \(2x^2+2x+1=0\)
\(\text{Δ}=2^2-4\cdot2\cdot1=4-8=-4< 0\)
Vì Δ<0 nên phương trình vô nghiệm
PT
1
CM
17 tháng 6 2019
TXĐ: D = [0; 2]
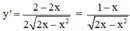
+ Hàm số đồng biến
⇔ y’ > 0
⇔ 0 < x < 1.
+ Hàm số nghịch biến
⇔ y’ < 0
⇔ 1 < x < 2.
Vậy hàm số đồng biến trên khoảng (0; 1), nghịch biến trên khoảng (1; 2).
T
10 tháng 10 2023
\(a)x^2-6x-2xy+12y\\=(x^2-2xy)-(6x-12y)\\=x(x-2y)-6(x-2y)\\=(x-2y)(x-6)\)
Bạn xem lại đề!
\(b\Big) (3-2x)(3+2x)+(2x+3)(2x-5)+4x\\=3^2-(2x)^2+(4x^2-10x+6x-15)+4x\\=9-4x^2+4x^2-10x+6x-15+4x\\=(9-15)+(-4x^2+4x^2)+(-10x+6x+4x)\\=-6\)
*Đã sửa đề*
\(c\Big) 4(x+1)^2+(2x-1)^2-8(x-1)(x+1)-4x\\=4(x^2+2x+1)+(2x)^2-2\cdot2x\cdot1x+1^2-8(x^2-1^2)-4x\\=4x^2+8x+4+4x^2-4x+1-8x^2+8-4x\\=(4x^2+4x^2-8x^2)+(8x-4x-4x)+(4+1+8)\\=13\)
*Đã sửa đề*
\(d\big) (3x+2)^2+(2x-7)^2-2(3x+2)(2x-7)-x^2+36x\\=[(3x+2)^2-2(3x+2)(2x-7)+(2x-7)^2]-x^2+36x\\=[(3x+2)-(2x-7)]^2-x^2+36x\\=(3x+2-2x+7)^2-x^2+36x\\=(x+9)^2-x^2+36x\\=(x+9-x)(x+9+x)+36x\\=9(2x+9)+36x\\=18x+81+36x\)
Bạn xem lại đề!
\(Toru\)
10 tháng 4 2023
`a,`
`f(x)=x^2+4x+10`
\(\text{Vì }\)\(x^2\ge0\left(\forall x\right)\)
`->`\(x^2+4x+10\ge10>0\left(\forall\text{ x}\right)\)
`->` Đa thức không có nghiệm (vô nghiệm).
`c,`
`f(x)=5x^4+x^2+` gì nữa bạn nhỉ? Mình đặt vd là 1 đi nha :v.
Vì \(x^4\ge0\text{ }\forall\text{ }x\rightarrow5x^4\ge0\text{ }\forall\text{ }x\)
\(x^2\ge0\text{ }\forall\text{ }x\)
`->`\(5x^4+x^2+1\ge1>0\text{ }\forall\text{ }x\)
`->` Đa thức vô nghiệm.
`b,`
`g(x)=x^2-2x+2017`
Vì \(x^2\ge0\text{ }\forall\text{ }x\)
`->`\(x^2-2x+2017\ge2017\text{ }\forall\text{ }x\)
`->` Đa thức vô nghiệm.
`d,`
`g(x)=4x^2004+x^2018+1`
Vì \(x^{2004}\ge0\text{ }\forall\text{ }x\rightarrow4x^{2004}\ge0\text{ }\forall\text{ }x\)
\(x^{2018}\ge0\text{ }\forall\text{ }x\)
`->`\(4x^{2004}+x^{2018}+1\ge1>0\text{ }\forall\text{ }x\)
`->` Đa thức vô nghiệm.
MM
0
CM
8 tháng 1 2017
Biểu thức x + 1 x 2 xác định khi x ≠ 0
Biểu thức x 2 + 1 x 2 + 2 x + 1 1 x + 1 xác định khi x ≠ 0 và x ≠ - 1
Với điều kiện x ≠ 0 và x ≠ - 1, ta có:
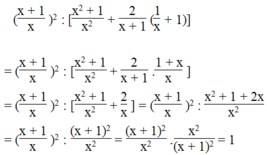
Vậy giá trị của biểu thức x + 1 x 2 : x 2 + 1 x 2 + 2 x + 1 1 x + 1 bằng 1 với mọi giá trị x ≠ 0 và x ≠ -1.
Xét hiệu : \(2x-x^2-1 = -(x^2 -2x+1) = -(x-1)^2\)
Ta thấy \(\left(x-1\right)^2\ge0\forall x\Rightarrow-\left(x-1\right)^2\le0\)
\(=> ĐPCM\)
Ta có
\((x-1)^2>=0 \) với mọi x
\(x^2-2x+1>=0\)
\(x^2-2x>=-1\)
Chia cả hai vế cho -1 ta đc
\(2x-x^2<=1\) với mọi x
đpcm