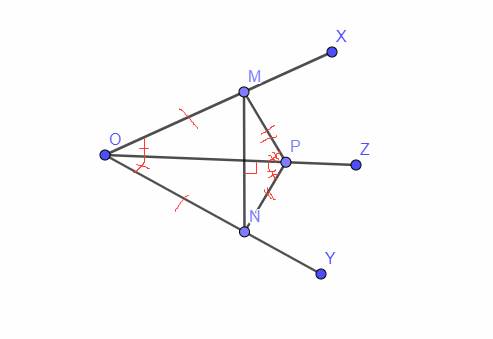
Cho góc xOy, trên tia Ox lấy điểm M, N (M nằm giữa O và N), Trên tia Oy lấy điểm P,Q( P nằm giữa O và Q) sao cho góc ONP = góc OQM. a) Chứng minh ∆ONP đồng dạng với ∆OQM b) Chứng minh OM.ON = OP.OQ c) Gọi I là giao điểm của PN và MQ. Chứng minh IM.IQ = IN.IP
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 5 2023
Xét ΔOQM và ΔOPN có
OQ=OP
góc O chung
OM=ON
=>ΔOQM=ΔOPN
=>góc OQM=góc OPN
6 tháng 2 2023
#\(N\)
`a,` Xét Tam giác `OMP` và Tam giác `ONP` có:
`OM = ON (g``t)`
\(\widehat{MOP}=\widehat{NOP}\) `(` tia phân giác \(\widehat{xOy}\) `)`
`OP` chung
`=>` Tam giác `OMP =` Tam giác `ONP (c-g-c)`
`b,` Vì Tam giác `OMP =` Tam giác `ONP (a)`
`=> MP = NP (` 2 cạnh tương ứng `)`
`=>`\(\widehat{MPH}=\widehat{NPH}\) `(` 2 góc tương ứng `)`
Xét Tam giác `MPH` và Tam giác `NPH` có:
`MP = NP (CMT)`
\(\widehat{MPH}=\widehat{NPH}(CMT)\)
`PH` chung
`=>` Tam giác `MPH = `Tam giác `NPH (c-g-c)`
`=>`\(\widehat{MHP}=\widehat{NHP}\) `(` 2 góc tương ứng `)`
Mà `2` góc này ở vị trí kề bù
`=>`\(\widehat{MHP}+\widehat{NHP}=180^0\)
`=>` \(\widehat{MHP}=\widehat{NHP}=\)\(\dfrac{180}{2}=90^0\)
`=>`\(MN\perp OP\left(đpcm\right)\)
7 tháng 11 2015
a) Xét tam giác OAD và OBC có: OA = OB; góc BOC chung; OD = OC
=> tam giác OAD = OBC ( c - g - c)
=> góc OAD = OBC
Mà góc CAD = 180o - OAD; góc CBD = 180o - OBC
Nên góc CAD = góc CBD
9 tháng 12 2021
a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
trứng rán ko cần mỡ,, bắp rang ko cần bơ,, nhưng mình cần shit { c... ] cơ
ooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooo Kucking hangson