giúp mik câu e và f bài 21 vs ạ 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. -2x(x3 - 3x2 - x + 1)
= -2x4 + 6x3 + 2x2 - 2x
c. 3x2(2x3 - x + 5)
= 6x5 - 3x3 + 15x2
Bài 3:
a: Ta có: \(6x\left(5x-3\right)+3x\left(1-10x\right)=7\)
\(\Leftrightarrow30x^2-18x+3x-30x^2=7\)
\(\Leftrightarrow x=-\dfrac{7}{15}\)
b: Ta có: \(3x\left(12x-4\right)-9x\left(4x-3\right)=30\)
\(\Leftrightarrow36x^2-12x-36x^2+27x=30\)
hay x=2
c: ta có: \(x\left(5-2x\right)-2x\cdot\left(x-1\right)=15\)
\(\Leftrightarrow5x-2x^2-2x^2+2x-15=0\)
\(\Leftrightarrow-4x^2+7x-15=0\)
\(\text{Δ}=7^2-4\cdot\left(-4\right)\cdot\left(-15\right)=-191\)
Vì Δ<0 nên phương trình vô nghiệm

\(e,\left(x-2\right)^2-16=0\\ \Leftrightarrow\left(x-6\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\\ f,x^2-5x-14=0\\ \Leftrightarrow\left(x-7\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=7\\x=-2\end{matrix}\right.\\ g,8x\left(x-3\right)+x-3=0\\ \Leftrightarrow\left(8x+1\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{8}\\x=3\end{matrix}\right.\)

Bài 20:
a, Độ dài cạnh còn lại của mảnh đất:
350 : 14 = 25 (m)
Chu vi mảnh đất:
2 x (14+25)= 78 (m)
b, Đổi: 15dm= 1,5m
Diện tích đất trồng cỏ:
1,5 x 25 x 2 + (14 - 1,5 x 2) x 1,5 x 2 = 108 (m2)
Diện tích mảnh đất:
25 x 14 = 350(m2)
Diện tích làm nhà:
350 - 108 = 242 (m2)
Đ.số:......


4.2:
a: x^2-x+1=x^2-x+1/4+3/4
=(x-1/2)^2+3/4>=3/4>0 với mọi x
=>x^2-x+1 ko có nghiệm
b: 3x-x^2-4
=-(x^2-3x+4)
=-(x^2-3x+9/4+7/4)
=-(x-3/2)^2-7/4<=-7/4<0 với mọi x
=>3x-x^2-4 ko có nghiệm
5:
a: x^2+y^2=25
x^2-y^2=7
=>x^2=(25+7)/2=16 và y^2=16-7=9
x^4+y^4=(x^2)^2+(y^2)^2
=16^2+9^2
=256+81
=337
b: x^2+y^2=(x+y)^2-2xy
=1^2-2*(-6)
=1+12=13
x^3+y^3=(x+y)^3-3xy(x+y)
=1^3-3*1*(-6)
=1+18=19

Bài 4:
a, F(\(x\)) = m\(x\) + 3 có nghiệm \(x\) = 2
⇔ F(2) = 0 ⇔ m.2 + 3 = 0
2m = -3
m = - \(\dfrac{3}{2}\)
b, F(\(x\)) = m\(x\) - 5 có nghiệm \(x\) = 3 ⇔ F(3) = 0
⇔3m - 5 = 0 ⇒ m = \(\dfrac{5}{3}\)
c, F(\(x\)) = \(x^2\) + a\(x\) + b có 2 nghiệm phân biệt \(x\) = 1; \(x\) = 0
⇔ \(\left\{{}\begin{matrix}0+0+b=0\\1+a+b=0\end{matrix}\right.\) ⇔ \(\left\{{}\begin{matrix}b=0\\a=-1\end{matrix}\right.\)

\(f,\Leftrightarrow x^3+2x^2+5x-2x^2-4x-10+2\left(x^2-4\right)-5x+10=0\\ \Leftrightarrow x^3-4x+2x^2-8=0\\ \Leftrightarrow x^3+2x^2-4x-8=0\\ \Leftrightarrow x^2\left(x-2\right)-4\left(x-2\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x-2\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)




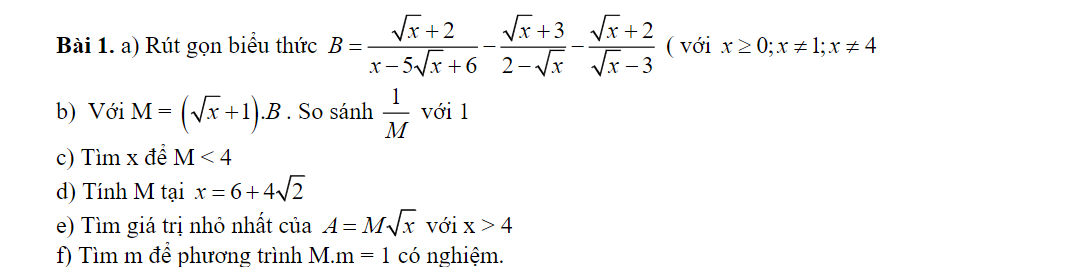 câu e và f cần giúp đỡ vs ạ
câu e và f cần giúp đỡ vs ạ 
 giúp mik câu c bài 3 và hết bài 4 vs ạ
giúp mik câu c bài 3 và hết bài 4 vs ạ
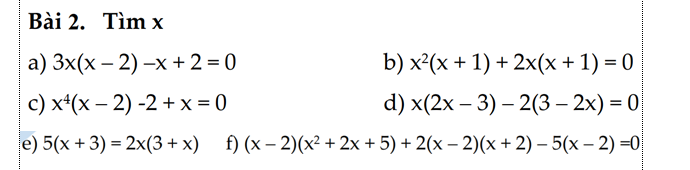 giúp mik câu f vs ạ
giúp mik câu f vs ạ


\(21,\\ e,PT\Leftrightarrow\left|2x-5\right|=5-2x\Leftrightarrow\left[{}\begin{matrix}2x-5=5-2x\left(x\ge\dfrac{5}{2}\right)\\5-2x=5-2x\left(x< \dfrac{5}{2}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\left(tm\right)\\0x=0\left(tm\right)\end{matrix}\right.\\ \Leftrightarrow x\in R\\ f,\Leftrightarrow\left|x-\dfrac{1}{4}\right|=\dfrac{1}{4}-x\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{1}{4}=\dfrac{1}{4}-x\left(x\ge\dfrac{1}{4}\right)\\\dfrac{1}{4}-x=\dfrac{1}{4}-x\left(x< \dfrac{1}{4}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{4}\left(tm\right)\\0x=0\left(tm\right)\end{matrix}\right.\\ \Leftrightarrow x\in R\)