Tìm số phức z biết (2-i)z = 4+3i
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 7 2019
Gọi z = a + bi với a , b ∈ ℝ
Khi đó phương trình z + z 1 + i + z - z 2 + 3 i = 4 - i trở thành:
2 a 1 + i + 2 b 2 + 3 i = 4 - i ⇔ 2 a + 4 b + 2 a + 6 b i = 4 - i
Do đó:
2 a + 4 b = 4 2 a + 6 b = - 1 a = 1 2 b = - 1 2 ⇒ z = 1 2 - 1 2 i
Ta có: w = z 3 + z + 1 z 2 + 1 - = z + 1 z 2 + 1 Thay 1 2 - 1 2 i vào ta được:
w = 1 2 - 1 2 i + 1 1 2 - 1 2 i 2 + 1 = 1 2 - 1 2 i + 1 - 1 2 i + 1 = 13 10 - 1 10 i
Suy ra w = 13 10 2 + - 1 10 2 = 170 10
Đáp án A
NK
1
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 4 2021
\(\Leftrightarrow\left(i^2+4i+4\right)\left(1-i\right)z=4-3i+\left(3+i\right)z\)
\(\Leftrightarrow\left(4i+3\right)\left(1-i\right)z-\left(3+i\right)z=4-3i\) (do \(i^2=-1\Rightarrow i^2+4=3\))
\(\Leftrightarrow\left(4i-4i^2+3-3i\right)z-\left(3+i\right)z=4-3i\)
\(\Leftrightarrow\left(7+i\right)z-\left(3+i\right)z=4-3i\)
\(\Leftrightarrow4z=4-3i\)
\(\Leftrightarrow z=1-\dfrac{3}{4}i\)
CM
31 tháng 8 2018
Chọn D.
Giả sử z=a+bi với a,b ∈ ℝ
Thay vào biểu thức ta được:
NL
2 tháng 6 2016
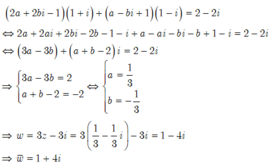
gọi z= a + bi \(\left(a,b\in R\right)\)
(2+i)(a+bi)=4-3i
\(\Leftrightarrow\) \(2a-b+\left(a+2b\right)i=4-3i\)
\(\Leftrightarrow\begin{cases}2a-b=4\\a+2b=-3\end{cases}\)
\(\Leftrightarrow\begin{cases}a=1\\b=-2\end{cases}\)
\(z=1-2i\)
w= i(1-2i) + 2( 1+ 2i) = 4 + 5i
LC
25 tháng 9 2016
Gọi \(z=a+bi\left(a,b\in R\right)\)
\(\left(2+i\right)\left(a+bi=4-3i\right)\)
\(\Leftrightarrow2a-b+\left(a+2b\right)i=4-3i\)
\(\Leftrightarrow\begin{cases}2a-b=4\\a+2b=-3\end{cases}\)
\(\Leftrightarrow\begin{cases}a=1\\b=-2\end{cases}\)
\(z=1-2i\)
\(w=i\left(1-2i\right)+2\left(1+2i\right)=4+5i\)
.
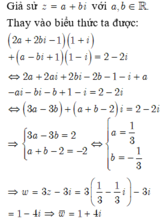
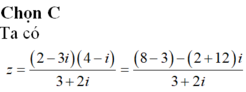
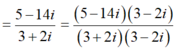
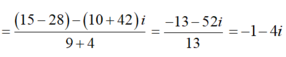
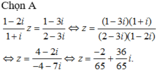
\(z=\frac{4+3i}{2-i}=\frac{\left(4+3i\right)\left(2+i\right)}{\left(2-i\right)\left(2+i\right)}=1+2i\)