ch 2 đường thẳng (d):y=4-2x và (d'):y=3x+1
a, ve (d) và (d') trên cùng 1 mặt phẳng tọa độ
b,gọi n là giao điểm của hai đường thẳng (d) và (d'). tìm tọa độ của điểm n
c.tính số đo góc ampha tạo bởi đường thẳng (d') vs trục ox
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 12 2023
a:
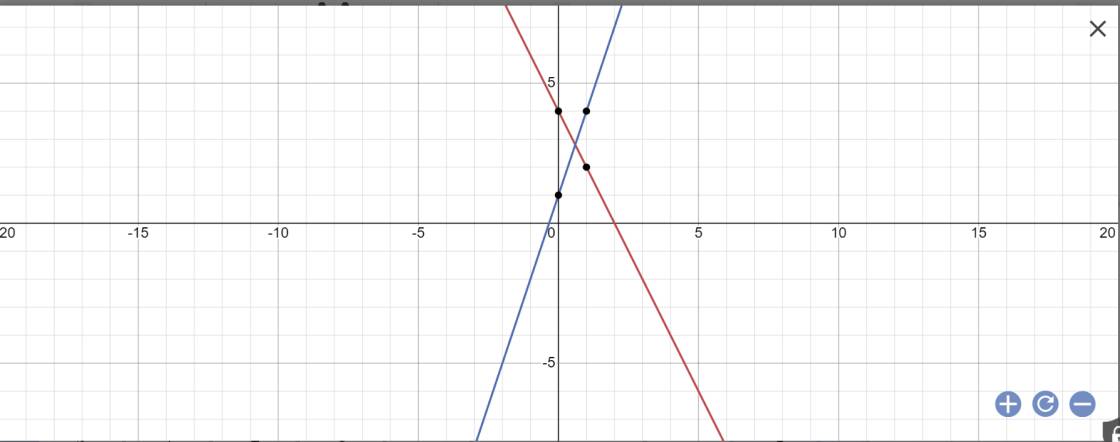
b: Phương trình hoành độ giao điểm là:
4-2x=3x+1
=>-2x-3x=1-4
=>-5x=-3
=>\(x=\dfrac{3}{5}\)
Thay x=3/5 vào y=3x+1, ta được:
\(y=3\cdot\dfrac{3}{5}+1=\dfrac{9}{5}+1=\dfrac{14}{5}\)
Vậy: \(N\left(\dfrac{3}{5};\dfrac{14}{5}\right)\)
c: (d'): y=3x+1
=>a=3
\(tan\alpha=a=3\)
=>\(\alpha\simeq71^034'\)
22 tháng 12 2021
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x+2=x\\y=x\end{matrix}\right.\Leftrightarrow x=y=-2\)
CM
26 tháng 12 2019
a) - Vẽ đồ thị hàm số y = 0,5x + 2 (1)
Cho x = 0 => y = 2 được D(0; 2)
Cho y = 0 => 0 = 0,5.x + 2 => x = -4 được A(-4; 0)
Nối A, D ta được đồ thị của (1).
- Vẽ đồ thị hàm số y = 5 – 2x (2)
Cho x = 0 => y = 5 được E(0; 5)
Cho y = 0 =>0 = 5 – 2x => x = 2,5 được B(2,5; 0)
Nối B, E ta được đồ thị của (2).
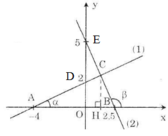
b) Ở câu a) ta tính được tọa độ của hai điểm A và B là A(-4 ; 0) và B (2,5 ; 0)
Hoành độ giao điểm C của hai đồ thị (1) và (2) là nghiệm của phương trình:
0,5 x + 2 = 5 - 2x
⇔ 0,5x + 2x = 5 – 2
⇔ 2,5.x = 3 ⇔ x = 1,2
⇒ y = 0,5.1,2 + 2 = 2, 6
Vậy tọa độ điểm C(1,2; 2,6).
c) AB = AO + OB = |-4| + |2,5| = 6,5 (cm)
Gọi H là hình chiếu của C trên Ox, ta có H( 1,2; 0)
Ta có: AH = AO + OH = 4 + 1,2 = 5,2
BH = BO – OH = 2,5 – 1,2 = 1,3
CH = 2,6
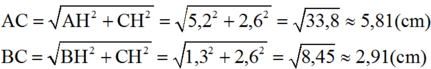
d) Gọi α là góc hợp bởi đường thẳng y = 0,5x + 2 với tia Ox.
Ta có: tgα = 0,5 => α = 26o34'
Gọi β là góc hợp bởi đường thẳng y = 5 - 2x với tia Ox
Tam giác OEB vuông tại O nên:
14 tháng 7 2023
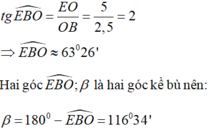
a: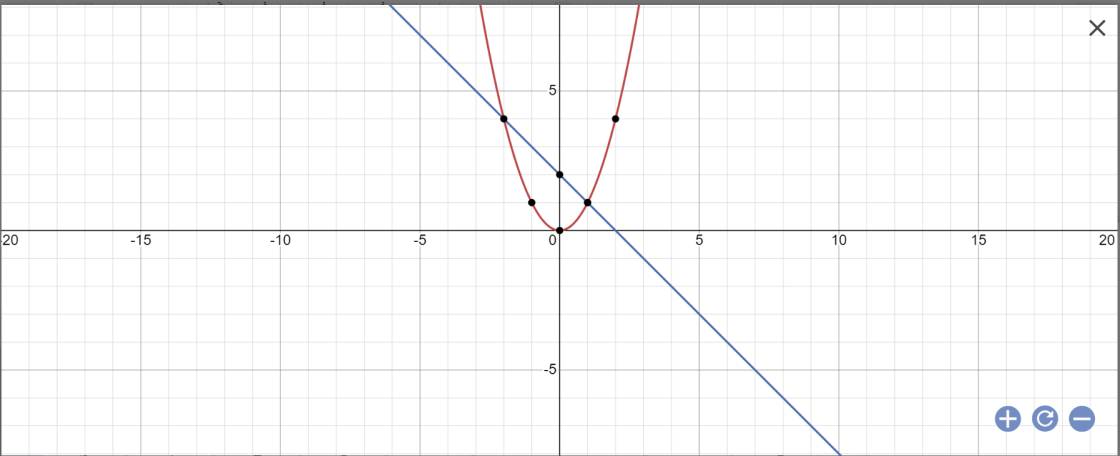 
b: PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1
DT
11 tháng 2 2022
c1:
Vì (d')//d nên pt đường thẳng của (d') là:y=-3x+b
đường thẳng (d') có tung độ gốc =2 => b=2
Vậy : pt đường thẳng của (d') là:y=-3x+2
14 tháng 12 2023
a:
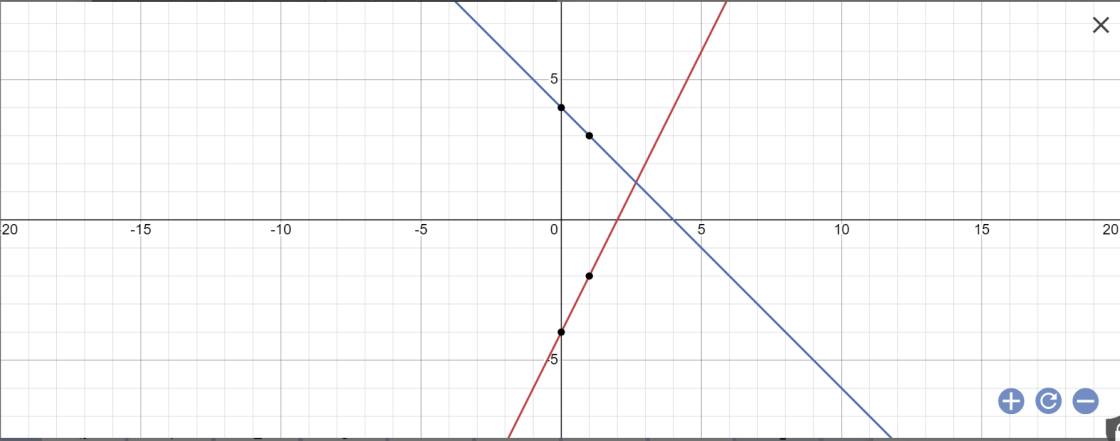
b: Tọa độ điểm Q là:
\(\left\{{}\begin{matrix}2x-4=-x+4\\y=-x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=8\\y=-x+4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{8}{3}\\y=-\dfrac{8}{3}+4=\dfrac{4}{3}\end{matrix}\right.\)
Vậy: \(Q\left(\dfrac{8}{3};\dfrac{4}{3}\right)\)
Tọa độ M là:
\(\left\{{}\begin{matrix}x=0\\y=2x-4=2\cdot0-4=-4\end{matrix}\right.\)
Vậy: M(0;-4)
Tọa độ N là:
\(\left\{{}\begin{matrix}x=0\\y=-x+4=-0+4=4\end{matrix}\right.\)
vậy: N(0;4)
Q(8/3;4/3); M(0;-4); N(0;4)
\(QM=\sqrt{\left(0-\dfrac{8}{3}\right)^2+\left(-4-\dfrac{4}{3}\right)^2}=\dfrac{8\sqrt{5}}{3}\)
\(QN=\sqrt{\left(0-\dfrac{8}{3}\right)^2+\left(4-\dfrac{4}{3}\right)^2}=\dfrac{8\sqrt{2}}{3}\)
\(MN=\sqrt{\left(0-0\right)^2+\left(4+4\right)^2}=8\)
Xét ΔMNQ có
\(cosMQN=\dfrac{QM^2+QN^2-MN^2}{2\cdot QM\cdot QN}=\dfrac{-1}{\sqrt{10}}\)
=>\(\widehat{MQN}\simeq108^026'\)
\(sinMQN=\sqrt{1-cos^2MQN}=\dfrac{3}{\sqrt{10}}\)
Diện tích tam giác MQN là:
\(S_{MQN}=\dfrac{1}{2}\cdot QM\cdot QN\cdot sinMQN\)
\(=\dfrac{1}{2}\cdot\dfrac{3}{\sqrt{10}}\cdot\dfrac{8\sqrt{5}}{3}\cdot\dfrac{8\sqrt{2}}{3}=\dfrac{32}{3}\)
29 tháng 7 2023
1:
a: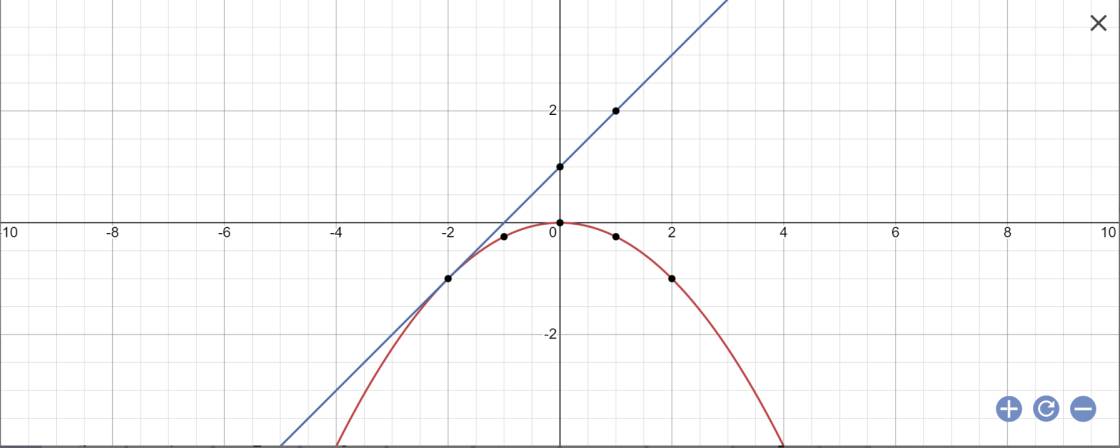 
b: PTHĐGĐ là:
-1/4x^2-x-1=0
=>x^2+4x+4=0
=>(x+2)^2=0
=>x=-2
=>y=-1/4*(-2)^2=-1
2: 3x-y=5 và 2x+3y=18
=>9x-3y=15 và 2x+3y=18
=>11x=33 và 3x-y=5
=>x=3 và y=3*3-5=4
a,tự vẽ
b) Xét phương trình hoành độ giao điểm của d và d':
4 - 2x = 3x + 1
<=> -2x - 3x = 1 - 4
<=> 5x = 3
<=> x = 3/5
=> y = 14/5