Cho ΔABC vuông tại A. Tia phân giác của góc B cắt AC tại M. Kẻ MD vuông góc
với BC tại D.
a) Chứng minh ΔABM = ΔDBM
b) Tia DM cắt tia BA tại E. Chứng minh rằng AC = DE
c) Chứng minh ΔAME = ΔDMC
d) Chứng minh BM vuông góc với AD
e) Kẻ AK vuông góc với ED tại K và DH vuông góc với AC tại H. Chứng minh
ΔAEK = ΔDCH
f) Tia AK và DH cắt nhau tại N. Chứng minh MN là tia phân giác của góc KMH
g) Chứng minh B, M, N thẳng hàng
h) Δ ABC thỏa mãn điều kiện gì để ΔADN là tam giác đều.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABM vuông tại A và ΔNDM vuông tại N có
MB=MD
góc AMB=góc NMD
=>ΔABM=ΔNDM
b: góc EDB=góc ABM
=>góc EBD=góc EDB
=>ΔEBD cân tại E

a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
=>DA=DE
b: Ta có: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
c: Xét ΔDAM vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADM}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAM=ΔDEC
=>DM=DC

a: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
\(\widehat{ABM}=\widehat{DBM}\)
Do đó: ΔBAM=ΔBDM
b: ΔBAM=ΔBDM
=>BA=BD và MA=MD
Xét ΔMAE vuông tại A và ΔMDC vuông tại D có
MA=MD
\(\widehat{AME}=\widehat{DMC}\)
Do đó: ΔMAE=ΔMDC
=>ME=MC
c: ΔMAE=ΔMDC
=>AE=DC
BA+AE=BE
BD+DC=BC
mà BA=BD
và AE=DC
nên BE=BC
Xét ΔABC vuông tại A và ΔDBE vuông tại D có
BC=BE
BA=BD
Do đó: ΔABC=ΔDBE
Ta có: BE=BC
=>B nằm trên đường trung trực của EC(1)
Ta có: ME=MC
=>M nằm trên đường trung trực của EC(2)
Xét ΔBEC có BE=BC
nên ΔBEC cân tại B
Ta có: ΔBEC cân tại B
mà BH là đường cao
nên BH là trung trực của EC(3)
Từ (1),(2),(3) suy ra B,M,H thẳng hàng

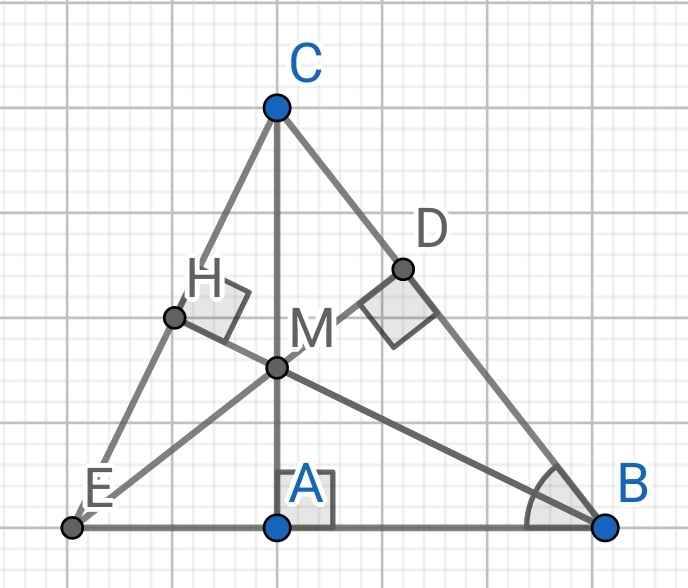 a) Do BM là tia phân giác của ABC (gt)
a) Do BM là tia phân giác của ABC (gt)
⇒ ∠ABM = ∠DBM
Xét hai tam giác vuông: ∆ABM và ∆DBM có:
BM là cạnh chung
∠ABM = ∠DBM (cmt)
⇒ ∆ABM = ∆DBM (cạnh huyền - góc nhọn)
⇒ BA = BD (hai cạnh tương ứng)
b) Xét hai tam giác vuông: ∆ABC và ∆DBE có:
BA = BD (cmt)
∠B chung
⇒ ∆ABC = ∆DBE (cạnh huyền - góc nhọn)
c) Do ∠ABM = ∠DBM (cmt)
⇒ ∠EBM = ∠CBM
Do ∆ABC = ∆DBE (cmt)
⇒ BC = BE (hai cạnh tương ứng)
Xét ∆MBE và ∆MBC có:
BE = BC (cmt)
∠EBM = ∠CBM (cmt)
BM là cạnh chung
⇒ ∆MBE = ∆MBC (c-g-c)
⇒ ME = MC (hai cạnh tương ứng)
c) ∆BCE có:
CA ⊥ AB (ABC vuông tại A)
⇒ CA ⊥ BE
⇒ CA là đường cao của ∆BCE (1)
MD ⊥ BC (gt)
⇒ ED ⊥ BC
⇒ ED là đường cao thứ hai của ∆BCE (2)
M là giao điểm của AC và ED
⇒ M là giao điểm của ba đường cao của ∆BCE
Mà BH ⊥ CE (gt)
⇒ BH là đường cao thứ ba của ∆BCE
⇒ B, M, H thẳng hàng

a) Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
\(\widehat{ABM}=\widehat{DBM}\)(BM là tia phân giác của \(\widehat{ABD}\))
Do đó: ΔBAM=ΔBDM(cạnh huyền-góc nhọn)
Suy ra: BA=BD(hai cạnh tương ứng)
Xét ΔABD có BA=BD(cmt)
nên ΔABD cân tại B(Định nghĩa tam giác cân)
b) Ta có: ΔBAM=ΔBDM(cmt)
nên MA=MD(hai cạnh tương ứng)
Ta có: BA=BD(cmt)
nên B nằm trên đường trung trực của AD(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: MA=MD(cmt)
nên M nằm trên đường trung trực của AD(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra BM là đường trung trực của AD(Đpcm)
c) Xét ΔAME vuông tại A và ΔDMC vuông tại D có
MA=MD(cmt)
\(\widehat{AME}=\widehat{DMC}\)(hai góc đối đỉnh)
Do đó: ΔAME=ΔDMC(cạnh góc vuông-góc nhọn kề)
Suy ra: ME=MC(hai cạnh tương ứng)
Xét ΔMEC có ME=MC(cmt)
nên ΔMEC cân tại M(Định nghĩa tam giác cân)
d) Ta có: ΔAME=ΔDMC(cmt)
nên AE=DC(hai cạnh tương ứng)
Ta có: BA+AE=BE(A nằm giữa B và E)
BD+DC=BC(D nằm giữa B và C)
mà BA=BD(cmt)
và AE=DC(cmt)
nên BE=BC
Xét ΔBEC có BE=BC(cmt)
nên ΔBEC cân tại B(Định nghĩa tam giác cân)
hay \(\widehat{BEC}=\dfrac{180^0-\widehat{EBC}}{2}\)(Số đo của một góc ở đáy trong ΔBEC cân tại B)(3)
Ta có: ΔBAD cân tại B(cmt)
\(\Leftrightarrow\widehat{BAD}=\dfrac{180^0-\widehat{ABD}}{2}\)(Số đo của một góc ở đáy trong ΔBDA cân tại B)
hay \(\widehat{BAD}=\dfrac{180^0-\widehat{EBC}}{2}\)(4)
Từ (3) và (4) suy ra \(\widehat{BAD}=\widehat{BEC}\)
mà \(\widehat{BAD}\) và \(\widehat{BEC}\) là hai góc ở vị trí đồng vị
nên AD//EC(Dấu hiệu nhận biết hai đường thẳng song song)

a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
Suy ra: \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)
hay DE\(\perp\)BC(Đpcm)
b) Ta có: ΔBAD=ΔBED(cmt)
nên AD=ED(hai cạnh tương ứng)
Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE(cmt)
\(\widehat{ADK}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔADK=ΔEDC(cạnh góc vuông-góc nhọn kề)
Suy ra: AK=EC(hai cạnh tương ứng)
c) Ta có: BA+AK=BK(A nằm giữa B và K)
BE+EC=BC(E nằm giữa B và C)
mà BA=BE(cmt)
và AK=EC(cmt)
nên BK=BC
Ta có: ΔADK=ΔEDC(cmt)
nên DK=DC(hai cạnh tương ứng)
Ta có: M là trung điểm của CK(cmt)
nên MK=MC
Ta có: BK=BC(cmt)
nên B nằm trên đường trung trực của KC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: DK=DC(cmt)
nên D nằm trên đường trung trực của KC(Tính chất đường trung trực của một đoạn thẳng)(2)
Ta có: CM=KM(cmt)
nên M nằm trên đường trung trực của KC(Tính chất đường trung trực của một đoạn thẳng)(3)
Từ (1), (2) và (3) suy ra B,D,M thẳng hàng(đpcm)

a) Xét tam giác ABC vuông tại A
\(AB^2+AC^2=BC^2\)
Thay số : \(AB^2=5^2-4^2=9\Rightarrow AB=3cm\)
b) Xét tam giác ABE và tam giác DBE có
\(\widehat{ABE}=\widehat{DBE}\left(gt\right)\)
\(\widehat{BAE}=\widehat{BDE}=90^o\)
BE chung
=> tam giác ABE = tam giác DBE (ch-gn)
c) Xét tam giác BMC có 2 đường cao CA và MD cắt nhau tại E
=> BE là đường cao thứ 3 của tam giác BMC
mà BE là phân giác của góc \(\widehat{ABC}\) hay \(\widehat{MBC}\)
=> tam giác BMC cân tại B (ĐPCM)
Câu C còn cách giả khác như sau
tam giác ABE = tam giác DBE (cmt)
=> AE = DE
Tam giác AME và DEC có
\(\widehat{MAE}=\widehat{CDE}=90^o\)
AE = DE
\(\widehat{AEM}=\widehat{DEC}\) (đối đỉnh)
=> tam giác AEM = tam giác DEC (g.c.g)
=> AM = DC
Có BA = BD (tam giác AEB = tam giác DEB)
AM = DC
=> BA + AM = BD + DC => BM = BC => tam giác BMC cân
À mà mình lớp 10 nha
a, Xét △ABM vuông tại A và △DBM vuông tại D
Có: BM là cạnh chung
∠ABM = ∠DBM (gt)
=> △ABM = △DBM (ch-gn)
b, Xét △ABC vuông tại A và △DBE vuông tại D
Có: AB = DB (△ABM = △DBM)
∠ABC là góc chung
=> △ABC = △DBE (cgv-gnk)
=> AC = DE (2 cạnh tương ứng)
c, Xét △AME vuông tại A và △DMC vuông tại D
Có: AM = MD (△ABM = △DBM)
∠AME = ∠DMC (2 góc đối đỉnh)
=> △AME = △DMC (cgv-gnk)
d, Vì AB = BD (cmt) => B thuộc đường trung trực của AD
Vì AM = DM (cmt) => M thuộc đường trung trực của AD
=> BM là đường trung trực của AD
=> BM ⊥ AD
e, Xét △DHC vuông tại K và △AKE vuông tại H
Có: DC = AE (△DMC = △AME)
∠DCH = ∠AEK (△ABC = △DBE)
=> △DHC = AKE (ch-gn)
f, Xét △AMK vuông tại K và △DMH vuông tại H
Có: AM = MD (cmt)
∠AMK = ∠DMH (2 góc đối đỉnh)
=> △AMK = △DMH (ch-gn)
=> MK = MH (2 cạnh tương ứng)
Xét △MKN vuông tại K và △MHN vuông tại H
Có: MK = MH (cmt)
MN là cạnh chung
=> △MKN = △MHN (ch-cgv)
=> ∠KMN = ∠HMN (2 góc tương ứng)
=> MN là phân giác KMH
g, Ta có: AK + KN = AN và DH + HN = DN
Mà AK = DH (△AMK = △DMH) ; KN = HN (△MKN = △MHN)
=> AN = DN
Xét △BAN và △BDN
Có: AB = BD (cmt)
AN = DN (cmt)
BN là cạnh chung
=> △BAN = △BDN (c.c.c)
=> ∠ABN = ∠DBN (2 góc tương ứng)
=> BN là phân giác ABD
Mà BM là phân giác ABD
=> BN ≡ BM
=> 3 điểm B, M, N thẳng hàng
h, Để △ADN là tam giác đều mà AN = DN (cmt)
<=> ∠AND = 60o <=> ∠ANM + ∠MND = 60o
Mà ∠ANM = ∠MND (△BAN = △BDN)
<=> ∠ANM = ∠MND = 30o
Vì AB ⊥ AC (gt) và DH ⊥ AC (gt) => DN ⊥ AC
=> AB // DN
=> ∠ABN = ∠BND (2 góc so le trong) và ∠ANB = ∠NBD (2 góc so le trong)
Mà ∠ANB = ∠BND = 30o (cmt)
=> ∠ABN = ∠NBD = 30o
=> ∠ABN + ∠NBD = 30o + 30o
=> ∠ABD = 60o
=> ∠ABC = 60o
Vậy để △ADN là tam giác đều khi △ABC có ∠ABC = 60o