Viết phương trình tiếp tuyến với (C): \(x^2+y^2-6x+2y+6=0\) biết tiếptuyến vuông góc với đường thẳng Δ: 2x+y-1=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 9 2018
Chọn A.
Tập xác định D = R \ {1}. Ta có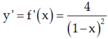 
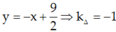
Vì tiếp tuyến vuông góc với Δ nên, 
Gọi N(xo; yo) là tọa độ tiếp điểm của tiếp tuyến, ta có f’(xo) = ktt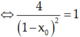 
⇔ (xo – 1)2 = 4 ⇔ xo = 3 ∨ xo = -1.
Với xo = 3 ⇒ y = -5, phương trình tiếp tuyến tại điểm này là:
⇔ y = -1(x – 3) – 5 ⇔ y = -x – 2
Với xo = -1 ⇒ y = -1, phương trình tiếp tuyến tại điểm này là:
⇔ y = -1(x + 1) – 1 ⇔ y = -x – 2.
HP
4 tháng 4 2021
a, Phương trình tiếp tuyến đi qua M: \(ax+by-3a+b=0\left(\Delta\right)\)
Đường tròn đã cho có tâm \(I=\left(1;-2\right)\) bán kính \(R=\sqrt{5}\)
Ta có: \(d\left(I;\Delta\right)=\dfrac{\left|a-2b-3a+b\right|}{\sqrt{a^2+b^2}}=\sqrt{5}\)
\(\Leftrightarrow\left(2a+b\right)^2=5\left(a^2+b^2\right)\)
\(\Leftrightarrow\left(a-2b\right)^2=0\)
\(\Leftrightarrow a=2b\)
\(\Rightarrow\Delta:2x+y-5=0\)
HP
4 tháng 4 2021
b, Phương trình tiếp tuyến: \(\left(d\right)2x-y+m=0\left(m\in R\right)\)
Ta có: \(d\left(I;d\right)=\dfrac{\left|2.1-1.\left(-2\right)+m\right|}{\sqrt{5}}=\sqrt{5}\)
\(\Leftrightarrow\left|m+4\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}m=1\\m=-9\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}d:2x-y+1=0\\d:2x-y-9=0\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 4 2021
1.
Tạo với Ox là tạo với tia Ox hay trục hoành nhỉ? 2 cái này khác nhau đấy. Tạo với tia Ox thì chỉ có 1 góc 60 độ theo chiều dương, tạo với trục hoành thì có 2 góc 60 và 120 đều thỏa mãn. Coi như tạo tia Ox đi
Đường tròn tâm \(I\left(-2;-2\right)\) bán kính \(R=5\)
\(tan60^0=\sqrt{3}\Rightarrow\) tiếp tuyến có hệ số góc bằng \(\sqrt{3}\Rightarrow\) pt có dạng:
\(y=\sqrt{3}x+b\Leftrightarrow\sqrt{3}x-y+b=0\)
\(d\left(I;d\right)=R\Leftrightarrow\dfrac{\left|-2\sqrt{3}+2+b\right|}{\sqrt{3+1}}=5\)
\(\Leftrightarrow\left|b+2-2\sqrt{3}\right|=10\Rightarrow\left[{}\begin{matrix}b=8+2\sqrt{3}\\b=-12+2\sqrt{3}\end{matrix}\right.\)
Có 2 tiếp tuyến: \(\left[{}\begin{matrix}\sqrt{3}x-y+8+2\sqrt{3}=0\\\sqrt{3}x-y-12+2\sqrt{3}=0\end{matrix}\right.\)
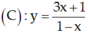
Đường tròn (C) có tâm \(I\left(3;-1\right)\) bán kính \(R=2\)
Gọi d là tiếp tuyến, do \(d\perp\Delta\) nên d nhận \(\left(1;-2\right)\) là 1 vtpt
Phương trình d có dạng: \(x-2y+c=0\)
Do d tiếp xúc (C) \(\Leftrightarrow d\left(I;d\right)=R\)
\(\Leftrightarrow\frac{\left|3.1-2.\left(-1\right)+c\right|}{\sqrt{5}}=2\)
\(\Leftrightarrow\left|c+5\right|=2\sqrt{5}\)
\(\Leftrightarrow\left[{}\begin{matrix}c+5=2\sqrt{5}\\c+5=-2\sqrt{5}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}c=-5+2\sqrt{5}\\c=-5-2\sqrt{5}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x-2y-5+2\sqrt{5}=0\\x-2y-5-2\sqrt{5}=0\end{matrix}\right.\)