Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 2:
Để hai đường thẳng này trùng nhau thì
\(\left\{{}\begin{matrix}k=5-k\\m-2=4-m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2k=5\\2m=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}k=\dfrac{5}{2}\\m=3\end{matrix}\right.\)
Hai đường thẳng y = kx + (m – 2) và y = (5 – k)x + (4 – m) trùng nhau khi và chỉ khi:
k = 5 – k (1) và m – 2 = 4 – m (2)
Từ (1) suy ra k = 2,5 (thỏa mãn điều kiện k ≠ 0 và k ≠ 5)
Từ (2) suy ra m = 3
Vậy với k = 2,5 và m = 3 thì hai đường thẳng trùng nhau.
Hai đường thẳng y = kx + (m – 2) và y = (5 – k)x + (4 – m) trùng nhau khi và chỉ khi:
k = 5 – k (1) và m – 2 = 4 – m (2)
Từ (1) suy ra k = 2,5 (thỏa mãn điều kiện k ≠ 0 và k ≠ 5)
Từ (2) suy ra m = 3
Vậy với k = 2,5 và m = 3 thì hai đường thẳng trùng nhau.
a: Để hai đường thẳng này cắt nhau thì \(2m+1< >2\)
=>\(2m\ne1\)
=>\(m\ne\dfrac{1}{2}\)
b: Để hai đường thẳng này song song thì \(\left\{{}\begin{matrix}2m+1=2\\2k-3\ne3k\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2m=1\\-k\ne3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{1}{2}\\k\ne-3\end{matrix}\right.\)
c: Để hai đường thẳng này trùng nhau thì \(\left\{{}\begin{matrix}2m+1=2\\2k-3=3k\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2m=1\\-k=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{1}{2}\\k=-3\end{matrix}\right.\)
Lời giải:
Để hai đường thẳng song song nhau thì:
\(\left\{\begin{matrix} k+3=4\\ m+1\neq 3-m\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} k=1\\ m\neq 1\end{matrix}\right.\)
Để hai đt cắt nhau thì: \(\left\{\begin{matrix} k+3\neq 4\\ m\in\mathbb{R}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} k\neq 1\\ m\in\mathbb{R}\end{matrix}\right.\)
Để hai đt trùng nhau thì: \(\left\{\begin{matrix} k+3=4\\ m+1=3-m\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} k=1\\ m=1\end{matrix}\right.\)
Để hai đt cắt nhau tại 1 điểm trên trục tung thì:
PT hoành độ giao điểm $(k+3)x+m+1=4x+3-m$ nhận $x=0$ là nghiệm
$\Leftrightarrow x(k-1)+(2m-2)=0$ nhận $x=0$ là nghiệm
$\Leftrightarrow 2m-2=0$
$\Leftrightarrow m=1$
Vậy $m=1$ và $k\in\mathbb{R}$ bất kỳ.
Để 2 đt vuông góc thì $(k+3).4=-1$ và $m$ bất kỳ
$\Leftrightarrow k=\frac{-13}{4}$ và $m$ bất kỳ.
Hàm số y = 2x + 3k có các hệ số a = 2, b = 3k.
Hàm số y = (2m + 1)x + 2k – 3 có các hệ số a' = 2m + 1, b' = 2k – 3.
Hai hàm số đã cho là hàm số bậc nhất nên 2m + 1 ≠ 0
a) Hai đường thẳng cắt nhau khi a ≠ a' tức là:
2 ≠ 2m + 1 ⇔ 2m ≠ 1
b) Hai đường thẳng song song với nhau khi a = a' và b ≠ b' tức là:
2 = 2m + 1 và 3k ≠ 2k – 3
c) Hai đường thẳng trùng nhau khi a = a' và b = b' tức là:
2 = 2m + 1 và 3k = 2k – 3
a) Hàm số \(y=2x+3k\) có các hệ số \(a=2,b=3k\)
Hàm số \(y=\left(2m+1\right)x+2k-3\) có các hệ số \(a'=2m+1,b'=2k-3\)
Hai hàm số đã cho là hàm số bậc nhất nên \(2m+1\ne0\)
\(\Leftrightarrow m\ne-\frac{1}{2}\)
Hai đường thẳng song song với nhau khi \(a=a'\) và \(b\ne b'\) tức là:
\(2=2m+1\) và \(3k\ne2k-3\)
Kết hợp với điều kiện trên ta có: \(m=\frac{1}{2}.k\ne-3\)
b) Hai đường thẳng song song:
\(\Leftrightarrow\hept{\begin{cases}2=2m+1\\3k\ne2k-3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m=\frac{1}{2}\\k\ne-3\end{cases}}\)
c) Hai đường thẳng trùng nhau:
\(\Leftrightarrow\hept{\begin{cases}2=2m+1\\3k=2k-3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m=\frac{1}{2}\\k=-3\end{cases}}\)
Hai đường thẳng y = kx + (m – 2) và y = (5 – k)x + (4 – m) trùng nhau khi và chỉ khi:
k = 5 – k (1) và m – 2 = 4 – m (2)
Từ (1) suy ra k = 2,5 (thỏa mãn điều kiện k ≠ 0 và k ≠ 5)
Từ (2) suy ra m = 3
Vậy với k = 2,5 và m = 3 thì hai đường thẳng trùng nhau.
Hai đường thẳng y = kx + (m – 2) và y = (5 – k)x + (4 – m) trùng nhau khi và chỉ khi:
k = 5 – k (1) và m – 2 = 4 – m (2)
Từ (1) suy ra k = 2,5 (thỏa mãn điều kiện k ≠ 0 và k ≠ 5)
Từ (2) suy ra m = 3
Vậy với k = 2,5 và m = 3 thì hai đường thẳng trùng nhau.
) và y = (3 - x) + 1 song song với nhau.
) và y = (5 - k)x + (4 - m) (với 
) trùng nhau? cắt nhau tại một điểm trên trục tung?
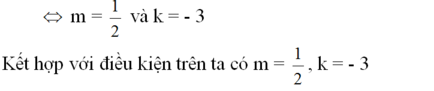
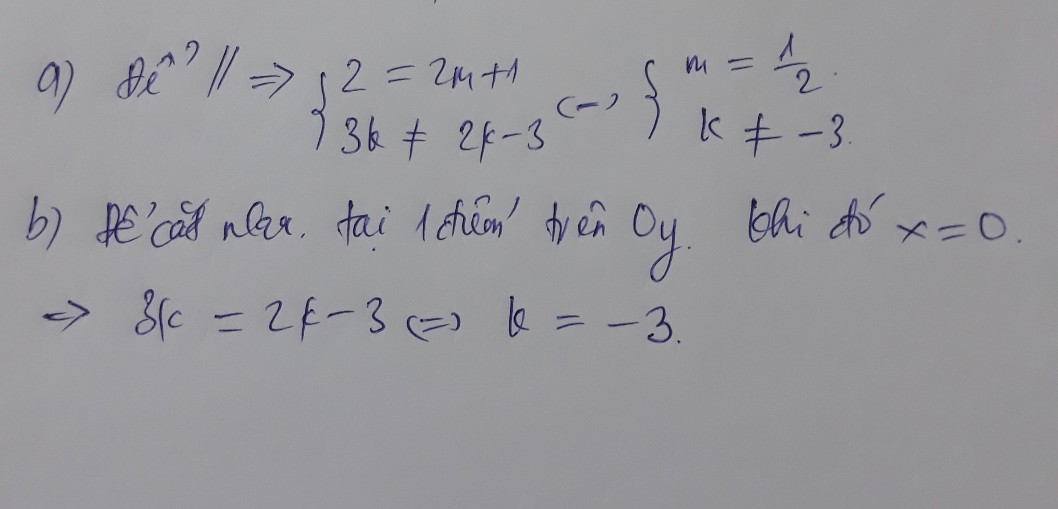
Để 2 đường thẳng trùng nhau \(\Rightarrow\left\{{}\begin{matrix}2k+6=-3\\2-m=m+1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}k=-\frac{9}{2}\\m=\frac{1}{2}\end{matrix}\right.\)
Để 2 đường thẳng song song \(\Rightarrow\left\{{}\begin{matrix}2k+6=-3\\2-m\ne m+1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}k=-\frac{9}{2}\\m\ne\frac{1}{2}\end{matrix}\right.\)
Để 2 đường thẳng cắt nhau \(\Rightarrow2k+6\ne-3\Rightarrow k\ne-\frac{9}{2}\)
Để 2 đường thẳng vuông góc \(\Rightarrow\left(2k+6\right).\left(-3\right)=1\Rightarrow k=-\frac{19}{6}\)