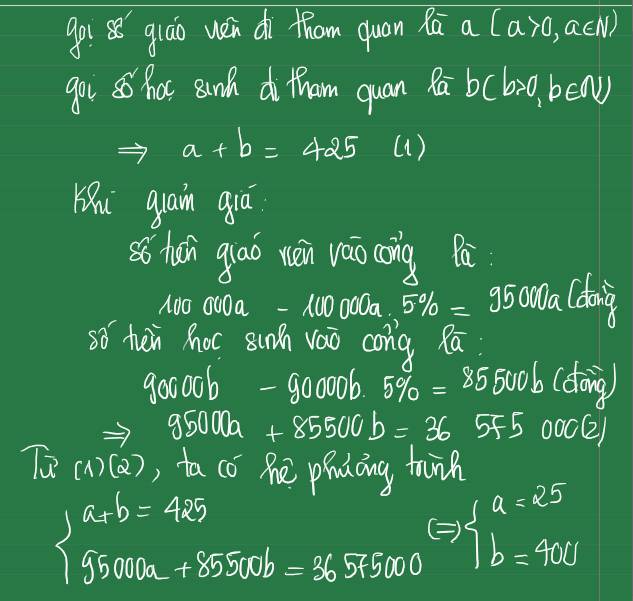Một công ty du lịch chào giá cho một suất đi tham quan khu du lịch Suối mơ Đồng Nai là 375000 đồng/ người. Nhà trường đã hợp đồng để công ty tổ chức cho 1 số giáo viên và học sinh đi tham quan. Công ty du lịch đã giảm 10% chi phí cho giáo viên và giảm 30% chi phí cho học sinh, nên tổng chi phí là 12487000 đồng. Tính sốlượng giáo viên và số lượng học sinh, biết số học sinh gấp 4 lần số giáo viên?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giá vé của 1 học sinh là 375000*0,7=262500 đồng
Giá vé của 1 giáo viên là 375000*0,9=337500 đồng
Gọi số học sinh và số giáo viên tham gia lần lượt là a,b
Theo đề, ta có hệ:
a=4b và 262500a+337500b=12487500
=>a=36 và b=9

a) Công ty sẽ giảm giá cho mỗi người 10 nghìn đồng khi cứ có thêm 1 khách tham gia ngoài 50 khách trên. Vậy số tiền mà công ty thu được theo x là: \((400000 - 10x).(50 + x)\)(đồng).
b) Số tiền công ty thu được chỉ với 50 khách ban đầu là: \(50.400000 = 20000000\) (đồng).
Số tiền công ty thu được sau khi thêm 10 người là:
\((400000 - 10.10000).(50 + 10) = 300000.60 = 18000000\)(đồng).
Ta thấy: 18 000 000 < 20 000 000 nên nếu số khách tăng thêm là 10 người thì số tiền công ty thu được là giảm so với số tiền thu được chỉ với 50 khách ban đầu.

Gọi 4a và a là số học sinh, giáo viên tham gia ( a ∈ N ∗ )
Giá vé của mỗi học sinh là 3 , 75.70 % = 2 , 625 (trăm nghìn đồng)
Giá vé của mỗi giáo viên là 3 , 75.90 % = 3 , 375 (trăm nghìn đồng)
Tổng số tiền là 124,875 (trăm nghìn đồng) nên ta có: 2 , 625.4 a + 3 , 375 a = 124 , 875
⇔ a = 9 (TM)
Vậy có 36 học sinh và 9 giáo viên đi.

Gọi số giáo viên và số học sinh tham gia lần lượt là a,b
Theo đề, ta có:
a=0,25b và 0,9*375000a+0,7*375000b=12487500
=>a=9; b=36

Gọi số giáo viên và số học sinh lần lượt là a,b
Theo đề, ta có: b=5a và 384000a+336000b=37152000
=>a=18 và b=90
Gọi b và 5b là tổng số giáo viên, học sinh t/gia ( b \(\in\) N*)
Gía vé của 1 học sinh là: 480 000 - ( 480 000 . 30%)= 336 000 ( đ )
Gía vé của 1 giáo viên là: 480 000 - ( 480 000 . 20%)= 384 000 ( đ )
Tổng chi phí khi giảm giá là 37 152 000 đ , ta có:
b384 000 đ + 5b336 000đ = 37 152 000 đ
b = 18
Số lượng giáo viên là: 18.5 = 90
Vậy số học sinh là 18, số lượng giáo viên là 90

a)
Do x là số lượng khách thứ 51 trở lên nên x>0.
Cứ thêm 1 người thì giá còn (300000-5 000.1) đồng/người cho toàn bộ hành khách.
Thêm x người thì giá còn (300 000-5 000.x) đồng/người cho toàn bộ hành khách.
Doanh thu theo x: \(\left( {50 + x} \right).\left( {300000 - 5000x} \right)\) (VNĐ)
b) Do chi phí thực sự cho chuyến đi là 15 080 000 đồng nên để công ty không bị lỗ thì doanh thu phải lớn hơn hoặc bằng 15 080 000 đồng
Khi đó:
\(\begin{array}{l}\left( {50 + x} \right).\left( {300000 - 5000x} \right) \ge 15080000\\ \Leftrightarrow \left( {50 + x} \right).5000.\left( {60 - x} \right) \ge 15080000\\ \Leftrightarrow \left( {x + 50} \right)\left( {60 - x} \right) \ge 3016\\ \Leftrightarrow - {x^2} + 10x + 3000 \ge 3016\\ \Leftrightarrow - {x^2} + 10x - 16 \ge 0\\ \Leftrightarrow {x^2} - 10x + 16 \le 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {x - 8} \right) \le 0\\ \Leftrightarrow 2 \le x \le 8\end{array}\)
Vậy số người của nhóm du khách nhiều nhất là 58 người.

Gọi x, y (người) lần lượt là số giáo viên và học sinh của trường \(\left(x,y\in N\circledast\right)\)
Vì trường tổ chức cho 330 người gồm giáo viên và học sinh đi tham quan Dinh Độc Lập nên: \(x+y=330_{\left(1\right)}\)
Vì nhân dịp kỷ niệm 90 năm Ngày thành lập Đoàn TNCS Hồ Chí Minh (26/3/1931 - 26/3/2021) do đó được giảm 10% cho mỗi vé vào tham quan và nhà trường chi phải trả số tiền là 6 480 000 đồng biết mối vé giáo viên là 40 000 đồng còn học sinh là 20 000 đồng, nên:
\(x\cdot40000\left(100\%-10\%\right)+y\cdot20000\left(100\%-10\%\right)=6480000_{\left(2\right)}\)
Từ (1) và (2), ta có hpt: \(\left\{{}\begin{matrix}x+y=330\\x\cdot40000\left(100\%-10\%\right)+y\cdot20000\left(100\%-10\%\right)=6480000\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=30\\y=300\end{matrix}\right.\)
Vậy có 30 giáo viên và 300 học sinh

Chọn A
Phương pháp:
Gọi giá tua là x (triệu đồng).
Lập hàm số tổng doanh thu theo x.
Xét hàm tìm GTLN của hàm số trên và kết luận.
Cách giải:
Gọi x (triệu đồng) là giá tua.
Số tiền được giảm đi so với ban đầu là 2-x.
Số người tham gia được tăng thêm nếu bán với giá x là: ![]()
Số người sẽ tham gia nếu bán giá x là: 150 + (400-200x) = 550 - 220x
Tổng doanh thu là: f(x) = x(550-220x) ![]()
![]()
Bảng biến thiên
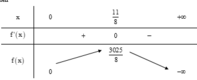
Dựa vào bảng biến thiên ta thấy f(x) đạt giá trị lớn nhất khi ![]()
Vậy công ty cần đặt gói tua 1375000 đồng thì tổng doanh thu sẽ cao nhất là 378125000 đồng.