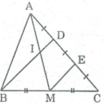
cho tam giác ABC M là điểm trên BC sao cho BM/BC=1/4.trên AM lâý điểm I sao cho AI/IM=1/2 và D là giao điểm của BI với AC tính tỉ số AD/BC ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:Áp dụng định lý Menelaus với tam giác $AMC$ có $B,I,D$ thẳng hàng:
$\frac{AD}{DC}.\frac{IM}{IA}.\frac{BC}{BM}=1$
$\Leftrightarrow \frac{AD}{DC}.2.3=1$
$\Leftrightarrow \frac{AD}{DC}=\frac{1}{6}$
$\Rightarrow \frac{AD}{DC}=\frac{1}{7}$

1: Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD

1: Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD

Gọi E là trung điểm của DC
Trong ΔBDC, ta có:
M là trung điểm của BC (gt)
E là trung điểm của CD (gt)
Nên ME là đường trung bình của ∆ BCD
⇒ME // BD (tính chất đường trung bình tam giác)
Suy ra: DI // ME
AD = 1/2 DC (gt)
DE = 1/2 DC (cách vẽ)
⇒ AD = DE và DI//ME
Nên AI= IM (tính chất đường trung bình của tam giác).

Gọi K là trung điểm của DC
Suy ra: AD=DK=KC
Xét ΔBDC có
M là trung điểm của BC
K là trung điểm của DC
Do đó: MK là đường trung bình của ΔBDC
Suy ra: MK//BD và \(MK=\dfrac{BD}{2}\)
hay ID//MK
Xét ΔAMK có
D là trung điểm của AK
DI//MK
Do đó: I là trung điểm của AM
hay IA=IM
