cho hbh ABCD có AB=2ad. Gọi I, k theo thứ tự là tđ của AB, CD. M là giao điểm của AK và DI. N là giao điểm của BK và CI. C/m tứ giác IMKN là hình chữ nhật.
mn ơi giúp mình vs mình cần gấp lắm :((
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 4 2022
a: Xét tứ giác ADFE có
AE//DF
AE=DF
Do đó: ADFE là hình bình hành
mà AE=AD
nên ADFE là hình thoi
mà \(\widehat{EAD}=90^0\)
nên ADFE là hình vuông
b: Ta có: ADFE là hình vuông
nên \(\widehat{EFD}=90^0\) và AF vuông góc với DE tại trung điểm của mỗi đường
Xét tứ giác BEFC có
BE//FC
BE=FC
Do đó: BEFC là hình bình hành
mà BC=BE
nên BEFC là hình thoi
mà \(\widehat{EBC}=90^0\)
nên BEFC là hình vuông
=>EC vuông góc với BF tại trung điểm của mỗi đường
Xét ΔEDC có
EF là đường trung tuyến
EF=DC/2
Do đó: ΔEDC vuông tại E
Xét ΔEDC có
EF là đường cao
EF là đường trung tuyến
DO đó: ΔEDC cân tại E
=>ED=EC
=>EM=EN
Xét tứ giác EMFN có \(\widehat{EMF}=\widehat{ENF}=\widehat{MEN}=90^0\)
nên EMFN là hình chữ nhật
mà EM=EN
nên EMFN là hình vuông
31 tháng 12 2018
a) E, F là trung điểm AB, CD ⇒ AE = EB = AB/2, DF = FC = CD/2.
Lại có AB = CD = 2.AD = BC.
⇒ AE = EB = BC = CF = FD = DA.
+ Tứ giác ADFE có AE // DF, AE = DF
⇒ ADFE là hình bình hành.
Hình bình hành ADFE có Â = 90º
⇒ ADFE là hình chữ nhật.
Hình chữ nhật ADFE là hình chữ nhật có AE= AD
⇒ ADFE là hình vuông.
b) Tứ giác DEBF có EB // DF, EB = DF nên là hình bình hành
Do đó DE // BF
Tương tự: AF // EC
Suy ra EMFN là hình bình hành
Theo câu a, ADFE là hình vuông nên ME = MF, ME ⊥ MF.
Hình bình hành EMFN có M̂ = 90º nên là hình chữ nhật.
Lại có ME = MF nên EMFN là hình vuông.
CM
12 tháng 12 2018
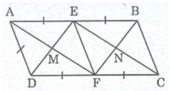
Tứ giác AEFD là hình thoi
⇒ AF ⊥ ED ⇒ ∠ (EMF) = 90 0
AF // CE (vì tứ giác AECF là hình bình hành)
Suy ra: CE ⊥ ED ⇒ ∠ (MEN) = 90 0
Xét tứ giác EBFD, ta có: EB = FD (vì cùng bằng AE)
EB // FD (vì AB // CD)
Tứ giác EBFD là hình bình hành (vì có một cặp cạnh đổi song song và bằng nhau) ⇒ DE // BF
Suy ra: BF ⊥ AF ⇒ ∠ (MFN) = 90 0
Vậy tứ giác EMFN là hình chữ nhật.
CM
29 tháng 5 2019
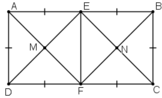
a) E, F là trung điểm AB, CD ⇒ AE = EB = AB/2, DF = FC = CD/2.
Ta có: AB = CD = 2AD = 2BC
⇒ AE = EB = BC = CF = FD = DA.
+ Tứ giác ADFE có AE // DF, AE = DF
⇒ ADFE là hình bình hành.
Hình bình hành ADFE có Â = 90º
⇒ ADFE là hình chữ nhật.
Hình chữ nhật ADFE là hình chữ nhật có AE= AD
⇒ ADFE là hình vuông.
b) Tứ giác DEBF có EB // DF, EB = DF nên là hình bình hành
Do đó DE // BF
Tương tự: AF // EC
Suy ra EMFN là hình bình hành
Theo câu a, ADFE là hình vuông nên ME = MF, ME ⊥ MF.
Hình bình hành EMFN có M̂ = 90º nên là hình chữ nhật.
Lại có ME = MF nên EMFN là hình vuông.
15 tháng 11 2016
a) Tứ giác ADFE có AE // DF, AE = DF nên là hình bình hành.
Hình bình hành ADFE có = 900 nên là hình chữ nhật.
Hình chữ nhật ADFE có AE = AD nên là hình vuông.
b) Tứ giác DEBF có EB // DF, EB = DF nên là hình bình hành.
Do đó DE // BF
Tương tự AF // EC
Suy ra EMFN là hình bình hành.
Theo câu a, ADFE là hình vuông nên ME = MF, ME ⊥ MF.
Hình bình hành EMFN có = 900 nên là hình chữ nhật, lại có ME = MF nên là hình vuông
16 tháng 11 2021
a: Xét tứ giác AICK có
AI//CK
AI=CK
Do đó: AICK là hình bình hành
5 tháng 1 2022
a: xét tứ giác ADFE có
AE//DF
AE=DF
Do đó: ADFE là hình bình hành
mà \(\widehat{EAD}=90^0\)
nên ADFE là hình chữ nhật
mà AE=AD
nên ADFE là hình vuông
c: Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
Suy ra: DE//BF và DE=BF(1)
hay ME//NF
Xét tứ giác BEFC có
BE//FC
BE=FC
Do đó: BEFC là hình bình hành
=>EC và BF cắt nhau tại trung điểm của mỗi đường
=>N là trung điểm của BF
=>FN=BF/2(2)
Ta có: AEFD là hình vuông
=>AF và DE vuông góc với nhau tại trung điểm của mỗi đường và bằng nhau
=>M là trung điểm của DE
=>EM=DE/2(3)
Từ (1), (2) và (3) suy ra EM=FN
Xét tứ giác EMFN có
EM//FN
EM=FN
Do đó: EMFN là hình bình hành
mà \(\widehat{EMF}=90^0\)
nên EMFN là hình chữ nhật