Cho tứ giác ABCD, goi E là giao điểm của 2 đường chéo . \(\Delta AED~\Delta BEC\). Gọi H, K thứ tự là chân đường vuông góc hạ từ I đến AD, BC . M , N thứ tự là trung điểm AB, CD. CMR : MN\(\perp\)HK
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta co:IA =IB(gt) ; HA =HC(gt)
Suy ra:HI la` đg tb của tam giac ABC
Suy ra:IH =1/2BC ;IH//BC (1)
Trong tam giac BDC co:KD =KB(gt) ;JD =JC(gt)
Suy ra :KJ la đg tb cu`a tam giac BDC
Suy ra :KJ =1/2BC ;KJ//BC (2)
Tu (1) va (2) suy ra :KJ = IH ;KJ // IH
Suy ra :tu giac KIHJ la hinh binh hanh(2 canh doi song song va bang nhau)(*)
Trong tam giac ADC co:HA =HC(gt) ;JD = JC(gt)
Suy ra :HJ la đg tb của tam giac ADC
Suy ra :HJ = 1/2AD
Mà AD =BC(gt) ; HI = 1/2BC(c/m tren)
Suy ra :HJ = HI (**)
Tu (*) va (**) suy ra tu giac KIHJ la hinh thoi (hbh co 2 canh ke bang nhau)
Suy ra :IJ vuong goc voi KH

Bài 2:
a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{EAD}=90^0\)
Do đó: ADME là hình chữ nhật

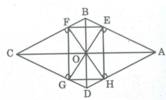
Ta có: AB // CD (gt)
OE ⊥ AB (gt)
⇒ OE ⊥CD
OG ⊥CD(gt)
Suy ra OE trùng với OG nên ba điểm O,E,G thẳng hàng.
BC // AD (gt)
OF ⊥ BC (gt)
⇒ OF ⊥ AD
OH ⊥ AD (gt)
Suy ra OF trùng với OH nên ba điểm O,H,F thẳng hàng.
Vì AC và BD là đường phân giác các góc của hình thoi nên:
OE = OF ( t/chất tia phân giác) (1)
OE = OH ( t/chất tia phân giác) (2)
OH = OG ( t/chất tia phân giác) (3)
Tứ giác EFGH có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên nó là hình chữ nhật.

ABCD là hình thoi
=>AC vuông góc với BD tại trung điểm của mỗi đường
=>AC\(\perp\)BD tại O và O là trung điểm chung của AC và BD
Ta có:ABCD là hình thoi
=>AB//CD và AD//BC và AB=BC=CD=DA
Xét ΔEBO vuông tại E và ΔGDO vuông tại G có
BO=DO
\(\widehat{EBO}=\widehat{GDO}\)
Do đó: ΔEBO=ΔGDO
=>EO=GO
Ta có: ΔEBO=ΔGDO
=>\(\widehat{EOB}=\widehat{GOD}\)
mà \(\widehat{GOD}+\widehat{GOB}=180^0\)(hai góc kề bù)
nên \(\widehat{EOB}+\widehat{GOB}=180^0\)
=>E,O,G thẳng hàng
mà OE=OG
nên O là trung điểm của EG
Xét ΔOHD vuông tại H và ΔOFB vuông tại F có
OD=OB
\(\widehat{ODH}=\widehat{OBF}\)(hai góc so le trong, AD//BC)
Do đó: ΔOHD=ΔOFB
=>OH=OF
Ta có; ΔOHD=ΔOFB
=>\(\widehat{HOD}=\widehat{FOB}\)
mà \(\widehat{FOB}+\widehat{FOD}=180^0\)
nên \(\widehat{HOD}+\widehat{FOD}=180^0\)
=>H,O,F thẳng hàng
mà OH=OF
nên O là trung điểm của HF
ABCD là hình thoi
=>AC là phân giác của góc BAD
=>\(\widehat{BAC}=\widehat{DAC}\)
Xét ΔAEO vuông tại E và ΔAHO vuông tại H có
AO chung
\(\widehat{EAO}=\widehat{HAO}\)
Do đó: ΔAOE=ΔAOH
=>OH=OE
mà \(OH=\dfrac{HF}{2};OE=\dfrac{EG}{2}\)
nên HF=EG
Xét tứ giác EFGH có
O là trung điểm chung của EF và GH
=>EFGH là hình bình hành
Hình bình hành EFGH có HF=EG
nên EFGH là hình chữ nhật

Bạn nào cần thì xem nè ( đợi lâu quá trời luôn mà không có ai trả lời mình hết )
Gọi I,J lần lượt là trung điểm của EC và ED.
Ta có tứ giác EINJ là hình bình hành ⇒EJ=NI,EI=NJ và ∠EIN=∠EJN.
Chú ý các tam giác CKE,DHE vuông tại K,H, theo tính chất đường trung tuyến
⇒JH=JE=IN,IK=IE=JN
Ta có KIC,HJD là các tam giác cân tại I và J, từ đó
∠KIE=2∠ACB=2∠ADB=∠HJE⇒∠KIN=∠HJN.
Do đó △KIN=△NJH (c.g.c)⇒NK=NH.
Chứng minh tương tự MH=MK⇒MN là đường trung trực của HK.
Bởi vậy HK⊥MN