Question

[Siêu sao bóng đá]

Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều, cạnh AB=6cm và thể tích của lăng trụ là 90\(\sqrt{3}\) cm³

a) Tính chiều cao của lăng trụ đó.

b) Tính diện tích mặt bên ABB'A'.

Answer 1

[Akai Haruma]

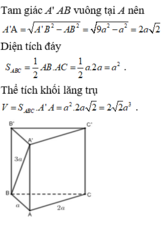
Lời giải:

a) Diện tích tam giác đều cạnh $a$ bằng: \(\frac{\sqrt{3}a^2}{4}\). Áp dụng vào bài:

\(S_{\text{đáy}}=S_{ABC}=\frac{\sqrt{3}.6^2}{4}=9\sqrt{3}\) (cm²)

Với $h$ là chiều cao:

\(V=S_{\text{đáy}}.h\Leftrightarrow 90\sqrt{3}=9\sqrt{3}.h\Rightarrow h=10\) (cm)

b) Do đây là lăng trụ đứng nên các cạnh bên đều là hình chữ nhật và vuông góc với đáy

$\Rightarrow ABB'A'$ là hình chữ nhật và $BB'=h$

$S_{ABB'A'}=AB.BB'=AB.h=6.10=60$ (cm²)

Answer 2

[Nguyễn Ngọc Lộc]

a, - Từ định lý hero ta có :

S_{đáy lăng trụ} = S_ABC = \(AB^2\frac{\sqrt{3}}{4}=6^2\frac{\sqrt{3}}{4}=9\sqrt{3}\left(cm^2\right)\)

- Ta lại có : V_{lăng trụ} = S_ABC .h = \(9\sqrt{3}.h=90\sqrt{3}\)

=> \(h=10\left(cm\right)\)

b, - Diện tích mặt bên ABB^,A^, là : \(AB.h=6.10=60\left(cm^2\right)\)