Tìm các cặp số (x,y) thỏa mãn 3x2+y2+2x-2y=1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DN
1
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 4 2022
\(3x^2+y^2+2x-2y-1=0\)
\(\Leftrightarrow x^2+2x\left(x+y\right)-2xy+y^2+2x-2y-1=0\)
\(\Leftrightarrow x^2+2-2xy+y^2+2x-2y-1=0\)
\(\Leftrightarrow\left(x-y\right)^2+2\left(x-y\right)+1=0\)
\(\Leftrightarrow\left(x-y+1\right)^2=0\)
\(\Leftrightarrow x-y+1=0\)
\(\Leftrightarrow y=x+1\)
Thế vào \(x\left(x+y\right)=1\)
\(\Rightarrow x\left(2x+1\right)=1\)
\(\Leftrightarrow2x^2+x-1=0\Rightarrow\left[{}\begin{matrix}x=-1\Rightarrow y=0\\x=\dfrac{1}{2}\Rightarrow y=\dfrac{3}{2}\end{matrix}\right.\)
CM
1 tháng 5 2019
Chọn C.
Phương pháp: Đưa bài toán về tìm m để hệ có nghiệm duy nhất.
CM
2 tháng 6 2017
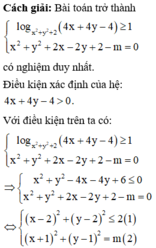
log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1
⇔ 4 x + 4 y - 4 ≥ x 2 + y 2 + 2 ⇔ x - 2 2 + y - 2 2 ≤ 2
Đây là tập hợp tất cả các điểm nằm trên và trong đường tròn tâm I(2;2) bán kính ℝ ' = m .
Ta có I I ' = 10 . m nhỏ nhất để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 thì hai đường tròn nói trên tiếp xúc ngoài
⇒ R + R ' = I I ' ⇔ m + 2 = 10 ⇔ m = 10 - 2 2
Đáp án cần chọn là B
LG
0
CM
21 tháng 2 2019
Đáp án A
Ta có, giả thiết
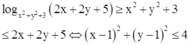
là miền trong đường tròn tâm I(1;1) bán kính R1 = 2
Và
T
1
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 3 2021
\(\Leftrightarrow2x^2-x+1=xy+2y\)
\(\Leftrightarrow2x^2-x+1=y\left(x+2\right)\)
\(\Leftrightarrow y=\dfrac{2x^2-x+1}{x+2}=2x-5+\dfrac{11}{x+2}\)
Do y nguyên \(\Rightarrow\dfrac{11}{x+2}\) nguyên \(\Rightarrow x+2=Ư\left(11\right)\)
Mà x nguyên dương \(\Rightarrow x+2\ge3\Rightarrow x+2=11\Rightarrow x=9\)
\(\Rightarrow y=14\)
Vậy \(\left(x;y\right)=\left(9;14\right)\)
Có 3x^2+y^2+2x-2y=1
=>9x^2+3y^2+6x-6y=3
=>(3x+1)^2+3(y-1)^2=7
=>3(y-1)^2 <=7
=> (y-1)^2<=7/3<2.333(3)
Mà (y-1)^2 là scp
=> (y-1)^2 thuộc 0,1
Sau đó xét 2 trg hợp và đối chiếu đk x thuộc Z
Chúc học tốt nhaaa