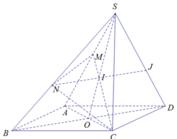
Cho hình bình hành ABCD nằm trong mp (P) và một điểm S nằm ngoài mp(P). Gọi M là điểm nằm giữa S và A ; N là điểm nằm giữa S và B; Giao điểm của hai đường thẳng AC và BD là O.
a) Tìm giao điểm của mp(CMN) với đường thẳng SO
b) Xác định giao tuyến của hai mặt phẳng (SAD) và (CMN)