Tính giá trị của tổng \(4+44+444+...+44...4\)( biết tổng có 2018 số hạng )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
Lời giải:
A = 4 9 9 + 99 + ... + 99...9 = 4 9 1 − 1 + 10 − 1 + 10 2 − 1 + .... + 10 2018 − 1 = 4 9 1 + 10 + 10 2 + ... + 10 2018 − 2019 = 4 9 10 2019 − 1 10 − 1 − 2019 = 4 9 10 2019 − 10 9 − 2018

4.4 < x < 4+44+444
=> 16 < x < 492
=> x={17;18;..;492}
Tổng của x là : [(492-17):1+1].[(492+17):2]=476.254,5=121142
Ta có 4*4 < x < 4+44+444
hay 16 < x < 492
\(\Rightarrow x\in\left\{17,18,...,491\right\}\)
Số số hạng của tập hợp trên là
( 491 - 17 ) : 1 + 1 = 475 (số)
Tổng là
( 491 + 17 ) *475 / 2 = 120650


Ta thấy
- Số thứ nhất có một chữ số 4
- Số thứ hai có hai chữ số 4
- Số thứ ba có ba chữ số 4
- Tương tự : 4444....44( 2000 chữ số bốn) => là số thứ 2000
đáp án tổng trên là........abcd
- d= 4*2000=.....0
- c=4*1999=.........6( nhớ 3)
- b= 4*1998=........2 cộng vói nhớ 3 trên =5(nhớ 3)
- a=4*1997=........8 công với nhớ 3 trên =1
=> abcd=1560


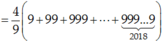
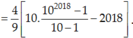
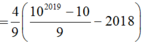
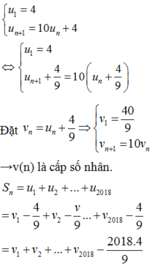
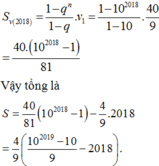

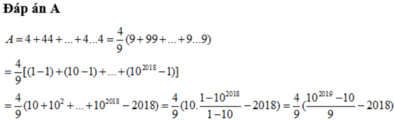
Lời giải:
Đặt \(\underbrace{11...1}_{n}=a\Rightarrow 9a+1=10^n\Rightarrow a=\frac{10^n-1}{9}\Rightarrow \underbrace{44...4}_{n}=4a=\frac{4}{9}(10^n-1)\)
Thay $n=1,2,...,2018$ và đặt tổng cần tính là $T$
Khi đó:
\(T=\frac{4}{9}(10^1-1)+\frac{4}{9}(10^2-1)+\frac{4}{9}(10^3-1)+...+\frac{4}{9}(10^{2018}-1)\)
\(=\frac{4}{9}(10+10^2+10^3+...+10^{2018}-2018)\)
\(10T=\frac{4}{9}(10^2+10^3+...+10^{2019}-20180)\)
Trừ theo vế:
\(9T=10T-T=\frac{4}{9}(10^{2019}-20180-10+2018)=\frac{4}{9}(10^{2019}-18172)\)
\(\Rightarrow T=\frac{4(10^{2019}-18172)}{81}\)