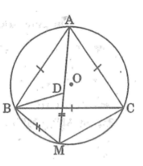
1. Cho tam giác đều ABC nội tiếp đường tròn ( O ), M là 1 điểm trên cung nhỏ BC.
a, chứng minh : MA= MB+ MC
b, Gọi E là giao điểm của MA với BC. Chứng minh : \(\frac{1}{ME}=\frac{1}{MC}+\frac{1}{MB}\)
c, Xác định vị trí của điểm M trên cung nhỏ BC sao cho \(\frac{1}{MC}+\frac{1}{MB}\) đạt giá trị nhỏ nhất
d, Kéo dài AB và CM cắt nhau tại P, BM và AC cắt nhau tại Q. Chứng minh rằng khi M chạy trên cung nhỏ BC ( không trùng với B và C) thì PQ luôn đi qua 1 điểm cố định