d đi qua M(4;1) và cắt tia Ox, Oy tại 2 điểm A, B sao cho diện tích tam giác OAB đạt giá trị lớn nhất. Viết phương trình đường thẳng d.
Cám ơn mọi người ạ!!! ♥️
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 4 2023
a: vtpt là (4;3)
Phương trình tổng quát là:
4(x-1)+3(y-2)=0
=>4x-4+3y-6=0
=>4x+3y-10=0
b: Phương trình Δ là:
2(x+2)+3(y-4)=0
=>2x+4+3y-12=0
=>2x+3y-8=0
c: Gọi (d): y=ax+b là phương trình cần tìm
Theo đề, ta có:
\(\left\{{}\begin{matrix}-2a+b=1\\3a+b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{5}\\b=\dfrac{7}{5}\end{matrix}\right.\)
d: Vì (d1)//(d) nên (d1): 3x-5y+c=0
Thay x=4 và y=-2 vào (d1), ta được:
c+3*4-5*(-2)=0
=>c=-22
f: (d): 2x-7y-1=0
=>Δ: 7x+2y+c=0
Thay x=3 và y=5 vào Δ, ta được:
c+21+10=0
=>c=-31
16 tháng 11 2021
a: Vì (d)//y=2x+4 nên m=2
Vậy: (d): y=2x+3-2n
Thay x=1 và y=2 vào (d), ta được:
5-2n=2
hay n=3/2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
2 tháng 11 2023
a, với d = -1
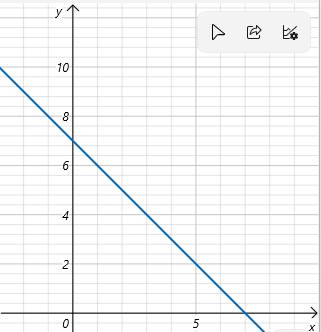
Ta có hàm số y = - \(x\) + 4 + 3 ⇒ y = -\(x\) + 7
+ Giao của đồ thị với trục o\(x\) là điểm có hoành độ thỏa mãn:
- \(x\) + 7 = 0 ⇒ \(x\) = 7
Giao đồ thì với trục o\(x\) là A(7; 0)
+ Giao của đồ thị với trục oy là điểm có tung độ thỏa mãn:
y = 0 + 7 ⇒ y = 7
Giao đồ thị với trục oy là điểm B(7; 0)
Ta có đồ thị
b, Đồ thị hàm số y = - m\(x\) + 4 - 3m (d)
(d) đi qua gốc tọa độ khi và chỉ tọa độ O(0; 0) thỏa mãn phương trình đường thẳng d
Thay tọa độ điểm O vào đường thẳng d ta có:
-m.0 + 4 - 3m = 0
4 - 3m = 0
m = \(\dfrac{4}{3}\)
c, để d cắt trục tung tại điểm - 4 khi và chỉ m thỏa mãn phương trình:
-m.0 + 4 - 3m = - 4
4 - 3m = - 4
3m = 8
m = \(\dfrac{8}{3}\)
d, d cắt trục tung tại điểm - 2 khi và chỉ khi m thỏa mãn phương trình
-m.0 + 4 - 3m = -2
4 - 3m = -2
3m = 6
m = 2
e, d song song với đường thẳng y = 2\(x\) + 3 khi và chỉ khi
- m = 2 và 4 - 3m ≠ 3 ⇒ m ≠ \(\dfrac{1}{3}\)
⇒m = -2
f, d đi qua A (1;2) khi và chỉ m thỏa mãn phương trình:
-m.(1) + 4 - 3m = 2
-m - 3m = 2 - 4
- 4m = -2
m = \(\dfrac{1}{2}\)
24 tháng 12 2021
\(a,\Leftrightarrow A\left(0;0\right)\in\left(d\right)\Leftrightarrow-2m+1=0\Leftrightarrow m=\dfrac{1}{2}\\ b,\Leftrightarrow x=3;y=4\Leftrightarrow3\left(m+1\right)-2m+1=4\\ \Leftrightarrow3m+3-2m+1=4\\ \Leftrightarrow m=0\Leftrightarrow\left(d\right):y=x+1\\ c,\text{PT hoành độ giao điểm: }x+1=-2x+4\Leftrightarrow x=1\Leftrightarrow y=2\Leftrightarrow B\left(1;2\right)\\ \text{Vậy }B\left(1;2\right)\text{ là giao 2 đths}\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 10 2019
Gọi đường thẳng cần tìm là \(y=kx+b\)
a/ \(\left\{{}\begin{matrix}-2k+b=1\\0.k+b=4\end{matrix}\right.\) \(\Rightarrow k=\frac{3}{2}\)
b/ Tọa độ giao điểm Q của d1 và d2: \(\left\{{}\begin{matrix}y=x-7\\y=-4x+3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=2\\y=-5\end{matrix}\right.\) \(\Rightarrow Q\left(2;-5\right)\)
\(\left\{{}\begin{matrix}-k+b=-3\\2k+b=-5\end{matrix}\right.\) \(\Rightarrow k=-\frac{2}{3}\)
CM
25 tháng 1 2018
Chọn (D) đường thẳng d đi qua điểm M và không đi qua điểm T.
13 tháng 10 2015
a) Gọi phương trình đường thẳng d là y = ax + b. Ta có: 5a + b = -1 và 6a + b = 4.
Do đó a = 5 và b = -26.
Vậy phương trình đường thẳng d là y = 5x - 26
b,c tương tự
Dễ thấy phương trình đường thẳng d có dạng : \(\frac{x}{a}+\frac{y}{b}=1\)\(\left(a,b>1\right)\)
Do d đi qua điểm \(M\left(4;1\right)\) nên ta có : \(\frac{4}{a}+\frac{1}{b}=1\)
Mặt khác ta có diện tích tam giác vuông ABO là \(S_{OAB}=\frac{1}{2}ab\)
Áp dụng bất đẳng thức Cô-si ta có : \(1=\frac{1}{a}+\frac{4}{b}\ge2\sqrt{\frac{1}{a}.\frac{4}{b}}=\frac{4}{\sqrt{ab}}\Leftrightarrow\sqrt{ab}\ge4\Leftrightarrow\frac{1}{2}ab\ge8\)
Vậy diện tích tam giác ABC nhỏ nhất là 8, dấu "=" xảy ra khi :
\(\left\{{}\begin{matrix}\frac{4}{a}=\frac{1}{b}\\\frac{4}{a}+\frac{1}{b}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=8\\b=2\end{matrix}\right.\)
sr bạn nhé mình chỉ tìm đc GTNN th ạ ^^
bạn bài này có nhầm đề k ạ tìm diện tính đạt lớn nhất hay nhỏ nhất v ạ