Chứng minh 2n+3 và 4n+3 là hai số nguyên tố cùng nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NM
Nguyễn Minh Quang
Giáo viên
23 tháng 11 2020
gọi a là ước chung lớn nhất của 2n+1 và 3n+2
do đó a phải là ước của \(2\left(3n+2\right)-3\left(2n+1\right)=1\) do đó a=1
hay 2n+1 và 3n+2 là hai số nguyên tố cùng nhau.
b.gọi b là ước chung lớn nhất của 2n+3 và 4n+5
do đó b phải là ước của \(2\left(2n+3\right)-\left(4n+5\right)=1\)do đó b=1
hay 2n+3 và 4n+5 là hai số nguyên tố cùng nhau
NK
28 tháng 12 2015
Gọi ƯCLN(2n + 3; 4n + 8) là d
=> 2n + 3 chia hết cho d => 2(2n + 3) chia hết cho d
4n + 8 chia hết cho d
Từ 2 điều trên => (4n + 8) - 2(2n + 3) chia hết cho d
=> 4n + 8 - 4n - 6 chia hết cho d
=> (4n - 4n) + (8 - 6) chia hết cho d
=> 2 chia hết cho d
=> d thuộc {1; 2}
Ta thấy 2n + 3 là lẻ mà 2n + 3 chia hết cho d nên d lẻ
=> d = 1
=> ƯCLN(2n + 3; 4n + 8) = 1
Vậy...
28 tháng 12 2015
Gọi ƯCLN(2n+3;4n+8)=d
Ta có: 2n+3 chia hết cho d=>2(2n+3) chia hết cho d=>4n+6 chia hết cho d
=>4n+8-(4n+6) chia hết cho d hay 2 chia hết cho d
mà 2n+3 lẻ, 4n+8 chẵn nên d=1
Vậy 2n+3 và 4n+8 là 2 số nguyên tố cùng nhau
L
1
23 tháng 11 2015
Gọi d > 0 là ước số chung của 2n+3 và 4n + 8
⇒ d ∈ Ư [2﴾2n + 3﴿ = 4n + 6]
﴾4n + 8﴿ ‐ ﴾4n + 6﴿ = 2
⇒ d ∈ Ư﴾2﴿ ⇒ d ∈ {1,2}
d = 2 không là ước số của số lẻ 2n+3
⇒ d = 1
vậy 2n+3 và 4n + 8 nguyên tố cùng nhau
ND
0
D
2
1 tháng 8 2017
Goi d là ƯCLN ( 2n + 3 ; 4n + 8 )
\(\Rightarrow\) 2n + 3 và 4n + 8 chia hết cho d
\(\Rightarrow\) 2 . ( 2n + 3 ) chia hết cho d
1 . ( 4n + 8 ) chia hết cho d
\(\Rightarrow\) 4n + 6 chia hết cho d
4n + 8 chia hết cho d
\(\Rightarrow\) 4n + 8 - ( 4n + 6 ) chia hết cho d
4n + 8 - ( 4n - 6 ) chia hết cho d
Suy ra 2 chia hết cho d .
d € Ư ( 2 ) = { 1 ; 2 }
Mà 2n + 3 không chia hết cho 2 . Suy ra d = 1
\(\Rightarrow\) ƯCLN ( 2n + 3 ; 3n + 4 ) = 1
Vậy 2n + 3 và 3n + 4 là 2 số nguyên tố cùng nhau .
1 tháng 8 2017
4n+8=2(2n+4)
2n+3,2n+4 ng tố cùng nhau 2 stn liên tiếp
k mình nha
TV
3
15 tháng 12 2019
bạn ơi hình như nhầm đề hai số này ko thể nguyên tố cùng nhau
13 tháng 12 2021
Giả sử: \(UCLN\left(2n+3;4n+8\right)=d\)
=> \(\left\{{}\begin{matrix}2n+3⋮d\\4n+8⋮d\end{matrix}\right.\) => \(\left\{{}\begin{matrix}4n+6⋮d\\4n+8⋮d\end{matrix}\right.\)
=> \(2⋮d\) => \(\left[{}\begin{matrix}d=1\\d=2\end{matrix}\right.\)
Có 2n+3 là số lẻ => \(2n+3⋮̸2\)
=> d = 1
=> đpcm
PT
1
CM
28 tháng 7 2017
Giả sử ƯCLN(2n+3 ;4n+8) = d
2 n + 3 ⋮ d 4 n + 8 ⋮ d ⇒ 2 2 n + 3 ⋮ d
=> 4 n + 8 - 2 2 n + 3 = 2 ⋮ d
=>d = 1 hoặc d = 2 .
Giả sử nếu d = 2 => (2n+3) ⋮ 2 (vô lý)
Vậy d = 1 hay 2n+3 và 4n+8 là hai số nguyên tố cùng nhau
PT
1
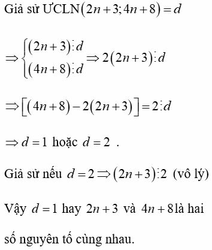
chtt
chtt