Question

[Bùi Lê Minh]

4: Cho ABC có đường trung tuyến AM. Đường phân giác của góc AMB cắt
cạnh AB ở E, đường phân giác của góc AMC cắt AC ở F.
a) Chứng minh:

EF // BC

b) Gọi I là giao điểm của EF và AM. Chứng minh I là trung điểm của EF
c) Biết AM = 7 cm, BC = 12 cm. Tính tỉ số diện tích hai tam giác AMF và MFC
d) Kẻ tia FM cắt tia AB tại K. Chứng minh rằng: KB.EA=KA.EB

Answer 1

[Trần Quốc Khanh]

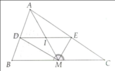
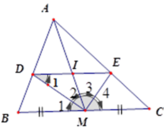
a/Có ME, MF là phân giác nên có:

\(\frac{AM}{BM}=\frac{AE}{EB}\left(1\right),\frac{AM}{MC}=\frac{AF}{FC}\left(2\right)\)

BM=MC nên (1)=(2) suy ra EF//BC(*)

b/Từ (*)\(\Rightarrow\frac{EI}{BM}=\frac{IF}{MC}\)( hệ quả Thales)

Mà BM=MC nên EI=IF

c/MC=1/2BC=1/2.12=6cm

Ta có: \(\frac{S_{AMF}}{S_{MFC}}=\frac{AM}{MC}=\frac{7}{6}\)

d/Trên tia đối FK lấy N sao cho AN//BM

Ta có: \(\frac{KB}{KA}=\frac{BM}{AN}=\frac{MC}{AN}\)(3)

Lại có: \(\frac{EB}{EA}=\frac{FC}{FA}\left(4\right)\)

Vì AN//MC nên (3)=(4)\(\Rightarrow\frac{KB}{KA}=\frac{EB}{EA}\RightarrowĐPCM\)