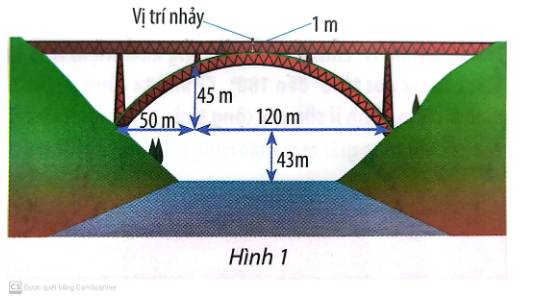
Trò chơi Bungee là trò chơi cảm giác mạnh, người chơi sẽ leo lên một nơi có địa thế cao như cây cầu, trực thăng ...rồi buộc dây đai quanh người và thả mình rơi tự do xuống mặt nước. Quãng đường rơi tự do không vận tốc ban đầu cho bởi công thức: S = ; Trong đó t là thời gian rơi tự do tính bằng giây, g là gia tốc trọng trường g 9,81 m/s 2 .
a) Lập công thức tính thời gian rơi tự do theo quãng đường.
b) Biết một vận động viên nhảy ở độ cao 320m, hỏi sau bao lâu thì vận động viên đó chạm mặt nước ? (Kết quả làm tròn đến chữ số thập phân thứ nhất)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Quãng đường người đó đi được sau n lần kéo là: \(100.{\left( {1 - 0,25} \right)^n}\)
Quãng đường người đó đi được sau 10 lần kéo là: \(100.{\left( {1 - 0,25} \right)^{10}} \approx 5,63\,\,\left( m \right)\)

Gọi \(y = f(x) = a{x^2} + bx + c\) là công thức của hàm số có đồ thị là hình ảnh của bộ phận chống đỡ.
Chọn hệ trục tọa độ Oxy như hình dưới:
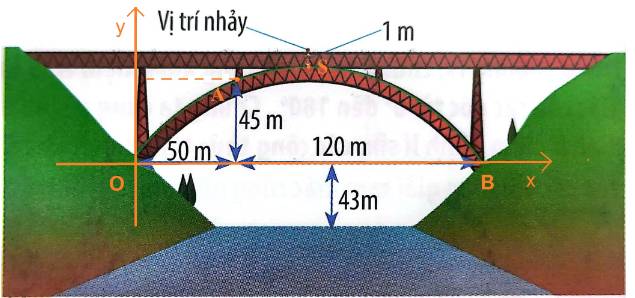
Gọi S là đỉnh của parabol, dưới vị trí nhảy 1m.
A, B là các điểm như hình vẽ.
Dễ thấy: A (50; 45) và B (120+50; 0) = (170; 0).
Các điểm O, A, B đều thuộc đồ thị hàm số.
Do đó:
\(f(0) = a{.0^2} + b.0 + c = 0 \Leftrightarrow c = 0\)
\(f(50) = a{.50^2} + b.50 + c = 45 \Leftrightarrow a{.50^2} + b.50 = 45\)
\(f(170) = a{.170^2} + b.170 + c = 0 \Leftrightarrow a{.170^2} + b.170 = 0 \Leftrightarrow a.170+ b = 0\)
Giải hệ phương trình \(\left\{ \begin{array}{l}a{.50^2} + b.50 = 45\\a.170 + b = 0\end{array} \right.\) ta được \(a = - \frac{{3}}{{400}};b = \frac{{51}}{{40}}\)
Vậy \(y = f(x) = - \frac{{3}}{{400}}{x^2} + \frac{{51}}{{40}}x\)
Đỉnh S có tọa độ là \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - \frac{{51}}{{40}}}}{{2.\left( { - \frac{{3}}{{400}}} \right)}} = 85;\;{y_S} = - \frac{{3}}{{400}}.8{5^2} + \frac{{51}}{{40}}.85 = \frac{{867}}{{16}} \approx 54,2\)
Khoảng cách từ vị trí bắt đầu nhảy đến mặt nước là: \(1 + 54,2 + 43 = 98,2(m)\)
Vậy chiều dài của sợi dây đó là: \(98,2:3 \approx 32,7\,(m)\)

a, Độ cao nảy ngược lên của người đó là một cấp số nhân có số hạng đầu \(u_1=9\) và công bội \(q=60\%=0,6\)
Độ cao nảy ngược lên của người đó ở lần nảy thứ ba là:
\(u_3=u_1\cdot q^2=9\cdot\left(0,6\right)^2=3,24\left(m\right)\)
b, Tổng các độ cao nảy ngược lên của người đó trong 5 lần này đầu là:
\(S_5=\dfrac{u_1\left(1-q^5\right)}{1-q}=\dfrac{9\cdot\left(1-0,6^2\right)}{1-0,6}=20,7504\left(m\right)\)

Vận tốc rơi tự do của vật khi đến mặt nước:
v = 2. g . s = 2.10.4 , 5 = 3 10 m / s
Lực cản do nước tác dụng lên học sinh.
Áp dụng công thức:
Δ p = F . Δ t ⇒ F = m .0 − m v Δ t = − 60.3. 10 0 , 5 = − 1138 , 42 N
Chọn đáp án A

Vận tốc rơi tự do của vật khi đến mặt nước:
v = 2. g . s = 2.10.4 , 5 = 3 10 ( m / s )
Lực cản do nước tác dụng lên học sinh.
Áp dụng công thức
Δ p = F . Δ t ⇒ F = m .0 − m v Δ t = − 60.3. 10 0 , 5 = − 1138 , 42 ( N )

Mình nghĩ là :
1 trong 2 người làm hành động :
Viết chữ " Bạn thua rồi và tôi thắng bạn "
Vì vậy , 1 trong 2 bạn đó thắng ( do người còn lại phải nói đúng rồi , nếu không nói thì vẫn thua )