3sinx-4cosx=-5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn A
y
=
3
sin
x
+
4
cos
x
+
5
⇔
3
sin
x
+
4
cos
x
+
5
−
y
=
0
Để phương trình có nghiệm thì 3 2 + 4 2 ≥ 5 − y 2
⇔
25
≥
25
−
10
y
+
y
2
⇔
y
2
−
10
y
≤
0
⇔
0
≤
y
≤
10
Vậy giá trị nhỏ nhất của hàm số là 0.

Lời giải:
Đặt \(3\sin x+4\cos x=t\)
Áp dụng BĐT Bunhiacopxky:
\(t^2=(3\sin x+4\cos x)^2\leq (3^2+4^2)(\sin ^2x+\cos ^2x)=25\)
\(\Rightarrow -5\leq t\leq 5\)
Với $t\in [-5;5]$ ta có:
\(y=3t^2+4t+1\leq 3.25+4.5+1=96\)
Mặt khác: \(y=3t^2+4t+1=3(t+\frac{2}{3})^2-\frac{1}{3}\)
\((t+\frac{2}{3})^2\geq 0, \forall t\in [-5;5]\Rightarrow y\geq -\frac{1}{3}\)
Vậy \(y_{\min}=\frac{-1}{3}; y_{\max}=96\)

a,Pt \(\Leftrightarrow cosx-sinx=\dfrac{1}{2}\)
\(\Leftrightarrow\sqrt{2}cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{2\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+arc.cos\left(\dfrac{1}{2\sqrt{2}}\right)+k2\pi\\x=-\dfrac{\pi}{4}-arc.cos\left(\dfrac{1}{2\sqrt{2}}\right)+k2\pi\end{matrix}\right.\) ,\(k\in Z\)
b) Pt \(\Leftrightarrow\dfrac{4}{5}cosx-\dfrac{3}{5}sinx=\dfrac{3}{5}\)
Đặt \(cosa=\dfrac{4}{5}\Rightarrow sina=\dfrac{3}{5}\)
Pttt:\(cosx.cosa-sina.sinx=\dfrac{3}{5}\)
\(\Leftrightarrow cos\left(x+a\right)=\dfrac{3}{5}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-a+arc.cos\left(\dfrac{3}{5}\right)+2k\pi\\x=-a-arc.cos\left(\dfrac{3}{5}\right)+2k\pi\end{matrix}\right.\)(\(k\in Z\))
Vậy...
c) Pt\(\Leftrightarrow\dfrac{3}{5}cos3x+\dfrac{4}{5}.sin3x=1\)
Đặt \(cosa=\dfrac{3}{5}\Rightarrow sina=\dfrac{4}{5}\)
Pttt:\(cos3x.cosa+sin3a.sina=1\)
\(\Leftrightarrow cos\left(3x-a\right)=1\)
\(\Leftrightarrow x=\dfrac{a}{3}+\dfrac{k2\pi}{3}\)(\(k\in Z\))
Vậy...
1)\(1+2sinx=2cosx\)
\(\Leftrightarrow cosx-sinx=\dfrac{1}{2}\)
\(\Leftrightarrow\left(cosx-sinx\right)^2=\dfrac{1}{4}\)
\(\Leftrightarrow cosx^2+sinx^2-2cosxsinx=\dfrac{1}{4}\)
\(\Leftrightarrow1-2cosxsinx=\dfrac{1}{4}\)
\(\Leftrightarrow2cosxsinx=\dfrac{3}{4}\)
\(\Leftrightarrow sin2x=\dfrac{3}{4}\)
\(\Rightarrow\left\{{}\begin{matrix}x=arcsin\dfrac{3}{8}+k\pi\\x=\pi-arcsin\dfrac{3}{8}+k\pi\end{matrix}\right.\) \(\left(K\in Z\right)\)
b) \(4cosx-3sinx=3\)
\(\Leftrightarrow\dfrac{4}{5}cosx-\dfrac{3}{5}sinx=\dfrac{3}{5}\)
Đặt \(cosa=\dfrac{3}{5},sina=\dfrac{4}{5}\)
Khi đó:
\(sinacosx-cosasinx=\dfrac{3}{5}\)
\(\Leftrightarrow sin\left(a-x\right)=\dfrac{3}{5}\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-x=arcsin\dfrac{3}{5}+k2\pi\\a-x=\pi-arcsin\dfrac{3}{5}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=a-arcsin\dfrac{3}{5}+k2\pi\\x=a-\pi-arcsin\dfrac{3}{5}+k2\pi\end{matrix}\right.\) \(\left(k\in Z\right)\)
3)\(3cos3x+4sin3x=5\)
\(\Leftrightarrow\dfrac{3}{5}cos3x+\dfrac{4}{5}sin3x=1\)
Đặt \(sina=\dfrac{3}{5},cosa=\dfrac{4}{5}\)
khi đó: \(sinacos3x+cosasin3x=1\)
\(\Leftrightarrow sin\left(a+3x\right)=\dfrac{\pi}{2}\)
\(\Leftrightarrow3x=\dfrac{\pi}{2}-a+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}-\dfrac{1}{3}a+k\dfrac{2}{3}\pi\),\(k\in Z\)
Chúc bạn học tốt^^

Đặt \(t=3sinx-4cosx=5\left(\frac{3}{5}sinx-\frac{4}{5}cosx\right)=5sin\left(x-a\right)\)
\(\Rightarrow-5\le t\le5\)
\(\Rightarrow y=t^2-t+m\)
\(y>0\) ; \(\forall m\Leftrightarrow t^2-t+m>0\Leftrightarrow m>-t^2+t\) ; \(\forall m\)
\(\Leftrightarrow m>\max\limits_{\left[-5;5\right]}\left(-t^2+t\right)\)
Mà \(-t^2+t=-\left(t-\frac{1}{2}\right)^2+\frac{1}{4}\le\frac{1}{4}\)
\(\Rightarrow m>\frac{1}{4}\)

3sinx – 4cosx = 1 ⇔ 3/5sinx - 4/5cosx = 1/5.
⇔ sin(x – α) = 1/5 (với cosα = 3/5 , sinα = 4/5)
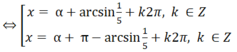
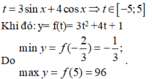
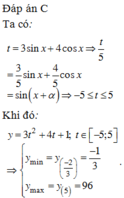

giúp mik vs ạ
chi 2 vế cho -5
<=>−35sinx+45cosx=1−35sinx+45cosx=1
đặt 35=sina35=sina
=>cosa=4545
=>cos(x+a)=1