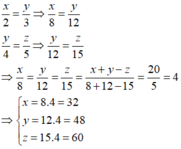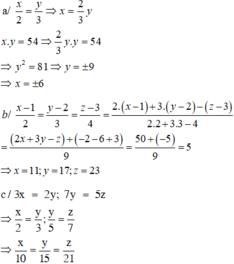tìm x,y,z thuộc Z+ biết x2+y3+z4=155
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
1
AH
Akai Haruma
Giáo viên
30 tháng 6 2023
Lời giải:
Ta thấy:
$(-x^2y^3)^2\geq 0$ với mọi $x,y$
$(2y^2z^4=2(yz^2)^2\geq 0$ với mọi $y,z$
$\Rightarrow (2y^2z^4)^3\geq 0$ với mọi $y,z$
Do đó để tổng $(-x^2y^3)^2+(2y^2z^4)^3=0$ thì:
$-x^2y^3=2y^2z^4=0$
Hay $(x,y,z)=(x,0,z)$ với $x,z$ bất kỳ hoặc $(x,y,z)=(0,y,0)$ với $y$ là số bất kỳ.
PT
1
CM
19 tháng 8 2018
Theo đề bài ta có :
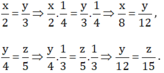
Do đó ta có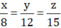 
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
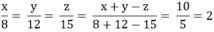
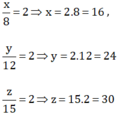
Vậy x =16 ; y = 24 ; z =30
NT
1
BB
28 tháng 12 2015
Ta có x2=y3\(\Rightarrow\) x/3=y/2;y5=z6\(\Rightarrow\) y/6=z/5 x/3=y/2\(\Rightarrow\) 1/3.x/3=1/3.y/2\(\Rightarrow\) x/9=y/6 (1) và y/6=z/5 (2). Từ (1) và (2)\(\Rightarrow\)x/9=y/6=z/5 \(\Rightarrow\) x^2/81=y^2/36=z^2/25=(x^2+y^2-z^2)/(81+36-25)=92/92=1 \(\Rightarrow\) x=9 hoặc -9 y=6 hoặc -6 và z=5 hoặc -5
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
9 tháng 7 2023
Bài 3:
a, (\(x\)+y+z)2
=((\(x\)+y) +z)2
= (\(x\) + y)2 + 2(\(x\) + y)z + z2
= \(x^2\) + 2\(xy\) + y2 + 2\(xz\) + 2yz + z2
=\(x^2\) + y2 + z2 + 2\(xy\) + 2\(xz\) + 2yz
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
9 tháng 7 2023
b, (\(x-y\))(\(x^2\) + y2 + z2 - \(xy\) - yz - \(xz\))
= \(x^3\) + \(xy^2\) + \(xz^2\) - \(x^2\)y - \(xyz\) - \(x^2\)z - y3
Đến dây ta thấy xuất hiện \(x^3\) - y3 khác với đề bài, em xem lại đề bài nhé
HT
1