Cho hcn ABCD .Qua A vẽ Ax//BD,Ax cắt đường thẳng CB tại E
a)CM:ABDE là hbh.
b)CM:tam giác ACE cân
c)Vẽ AM \(\perp\)BD(M\(\varepsilon\)BD) ,BN\(\perp\)AE (N thuộc AE).CM:AMBN là hcn
_Giup vs _
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 5 2020
a trứng rán cần mỡ bắp cần bơ yêu ko cần cớ cần cậu cơ
CM
29 tháng 4 2018
a, HS tự chứng minh
b, HS tự chứng minh
c, Tứ giác ACFK nội tiếp (I) với I là trung điểm của KF => BD là trung trực AC phải đi qua I
d, HS tự chứng minh
28 tháng 1 2022
a) Xét tam giác ABC có: OE // BC (gt).
\(\Rightarrow\) \(\dfrac{AE}{AB}=\dfrac{AO}{AC}\left(Talet\right).\left(1\right)\)
Xét tam giác ACD có: OF // CD (gt).
\(\Rightarrow\) \(\dfrac{AF}{AD}=\dfrac{AO}{AC}\left(Talet\right).\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\) \(\dfrac{AF}{AD}=\dfrac{AE}{AB}.\)
Xét tam giác ABD có: \(\dfrac{AF}{AD}=\dfrac{AE}{AB}\left(cmt\right).\)
\(\Rightarrow\) EF // BD (định lý Talet đảo).
CM
27 tháng 11 2017
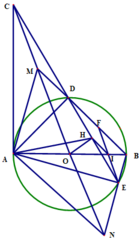
a) Ta có
C A B ⏜ = 90 0 O H C ⏜ = 90 0 ⇒ C A B ⏜ + O H C ⏜ = 180 0
Vậy tứ giác AOHC nội tiếp.
b) Ta có C A D ⏜ = A E C ⏜ , A C E ⏜ chung suy ra Δ A C D ~ Δ E C A (g.g)
⇒ C A C E = A D A E ⇒ A C . A E = A D . C E
c) Từ E vẽ đường thẳng song song với MN cắt cạnh AB tại I và cắt cạnh BD tại F ⇒ H E I ⏜ = H C O ⏜ .
Vì tứ giác AOHC nội tiếp ⇒ H A O ⏜ = H C O ⏜ = H E I ⏜ .
Suy ra tứ giác AHIE nội tiếp ⇒ I H E ⏜ = I A E ⏜ = B D E ⏜ ⇒ H I / / B D .
Mà H là trung điểm của DE=> I là trung điểm của EF. Có EF//MN và IE= IF
=> O là trung điểm của đoạn thẳng MN.
Suy ra tứ giác AMBN là hình bình hành => AM//BN.
a)Sai đề Sửa lại ADBE là hbh
Ta có AD//EB(vì AD//BC)
AE//BD(Vì Ax//BD)
=>ADBE là hbh(đpcm)
b)Vì ADBE là hbh =>AE=BD=>AC=AE=>ΔACE cân
c)Dễ dang C/m được △AMB=△ANB
=>AN=MB(1)
Mà AN//MB(vì AE//BD)(2)
Lại có ∠ANB=∠AMB(3)
Từ (1)(2)(3)=>AMBN là hcn